Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 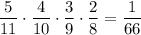 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна  . По теореме умножения
. По теореме умножения 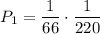
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 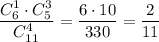 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 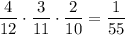 . По теореме умножения:
. По теореме умножения: 
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 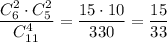 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 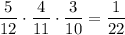 . По теореме умножения :
. По теореме умножения : 
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна  . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна  . По теореме умножения:
. По теореме умножения: 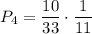
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 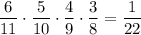 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 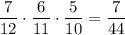 . По теореме умножения:
. По теореме умножения: 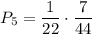
Итого, по теореме сложения:

Будем разбивать на несколько случаев.
1) Если из первой урны взяли 4 чёрных шара. Вероятность достать четыре чёрных шара равна 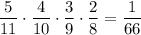 . Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна
. Тогда во второй урне будет 3 белых и 9 черных шаров. Вероятность того, что среди трех отобранных шаров из второй урны окажутся все белые равна  . По теореме умножения
. По теореме умножения 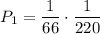
2) Если из первой урны взяли 1 белый шар и 3 чёрных. Вероятность такого события равна 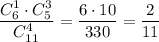 . Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна
. Тогда во второй урне будет 4 белых и 8 черных шаров. Вероятность того, что среди отобранных шаров из второй урны все белые равна 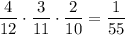 . По теореме умножения:
. По теореме умножения: 
3) Из первой урны взяли 2 белых шара и 2 чёрных. Вероятность такого события: 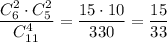 . Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна
. Во второй урне будет 5 белых и 7 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны все окажутся белыми равна 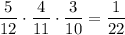 . По теореме умножения :
. По теореме умножения : 
4) Из первой урны взяли 3 белых шара и 1 чёрный шар. Вероятность достать 3 белых шара и 1 чёрный шар равна  . Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна
. Во второй урне останется 6 белых и 6 чёрных шаров. Вероятность того, что среди отобранных шаров из второй урны окажутся все белыми равна  . По теореме умножения:
. По теореме умножения: 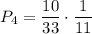
5) И, наконец, когда из первой урны урны взяли все четыре белых шаров. Вероятность такого события: 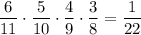 . Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна
. Во второй урне остается 7 белых и 5 черных шаров. Вероятность того, что среди отобранных 3 шаров из второй урны окажутся все белыми равна 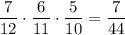 . По теореме умножения:
. По теореме умножения: 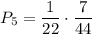
Итого, по теореме сложения:

Чтобы перевести дробное число в положительную степень нужно перенисти знаменатель в числитель и поменять снак степени то есть в первом у тебя вначале получалась такая дробь
13/6^-2
Когда ты перенесешь
у тебя получится
6/13^2=6/169
так же и все остальные делаешь ,получается
2)13/7^-2=7/13^2=7/169
3)30/7^-2=7/30^2=7/900
4)7/2^-2=2/7^2=2/49
Можешь поблагодарить и отметить как лучшее ,заранее большое