а) 4/9 и 7/15; (4*5)/(3*5*3) и (7*3)/(3*5*3); 20/45 < 21/45. Следовательно, 4/9< 7/15. Сумма 4/9+7/15=20/45+21/45=41/45. Разность 4/9-7/15=20/45-21/45=-1/45.
б) 3/750 и 9/250; 3/(250*3) и 9*3/(250*3); 3/750 < 27/750. Следовательно, 3/750 < 27/750. Сумма 3/750+9/250=3/750+27/750=30/750=3/75=1/25. Разность 3/750-9/250=3/750-27/750=-24/750.
в) (9*3)/(5*4*3) и (5*5)/(5*4*3); 27/60>25/60. Сумма 52/60=13/15. Разность 2/60.
г) 3/(3*2*2) и 13/(3*2*3); (3*3)/36 и (13*2)/36; 9/36<26/36. Сумма 35/36. Разность -17/36.
д) (2*9)/(97*2) и 13/194; 18/194>13/194. Сумма 31/194. Разность -4/197.
е) (5*13)/(25*5) и 8/125; 65/125>8/125. Сумма 73/125. Разность 57/125.
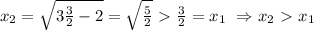
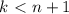
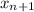 :
: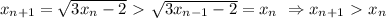

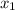 , по индукции получаем справедливость для любого
, по индукции получаем справедливость для любого 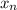 .
.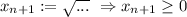 , потому можно извлечь корень)
, потому можно извлечь корень)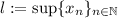 . Из (*) следует:
. Из (*) следует: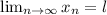 , но для больших
, но для больших 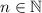 выполняется
выполняется 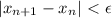 (Коши), следовательно
(Коши), следовательно 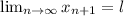
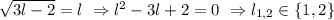
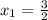 следует
следует 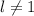 .
.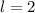
что за задача, вы живодеры?
Пошаговое объяснение:
смотри летело 1200 секунд, а поднялось на 10 метров