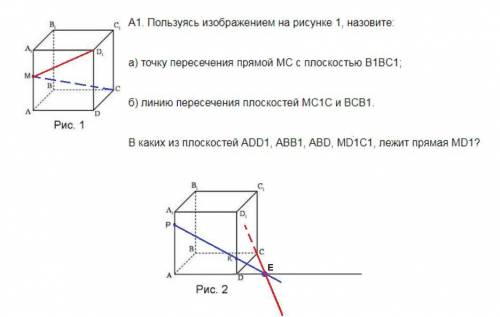
А1.
а) МС ∩ (В₁ВС) = С;
б) (МС₁С) ∩ (ВСВ₁) = СС₁, так как обе точки - С и С₁ - принадлежат двум плоскостям.
Прямая MD₁ лежит в тех плоскостях, в которых лежат обе точки - М и D₁: (ADD₁), (MD₁C₁)
A2.
а) РК лежит в плоскости (АА₁D), эта плоскость пересекает (АВС) по прямой AD. Поэтому находим точку пересечения прямых AD и РК - точку Е. Это и есть точка пересечения прямой РК и плоскости (АВС).
РК ∩ (АВС) = Е.
б) Чтобы построить линию пересечения плоскостей (РКС) и (ADC) надо найти или построить две точки, принадлежащие этим двум плоскостям.
Точка Е лежит на прямых РК и AD, значит принадлежит двум плоскостям. Точка С принадлежит плоскости (РКС), это видно из названия, и плоскости (ADC). Значит ЕС - искомая прямая.
(РКС) ∩ (ADC) = ЕС.
Проведем в пирамиде сечение МSK.
МК - средняя линия треугольника CDB, она параллельна DB и равна ее половине.
Диагональ АС квадрата АВСD равна диагонали DB
ОР - четверть этой диагонали и равна 8:4=2-это мы видим из треугольника CDB, в котором высота делится отрезком МК пополам.
SР- высота, биссектриса и медиана треугольного сечения МSK.
tg ∠ SPo=SP:OP=13:2=6,5