] для данной геометрической прогрессии а(1)=2
тогда а(5)=162
а(5)=а(1)*q^4 , где q - знаменатель прогресии
найдем q
162=2*q^4
q^4=81
q=3
Сумма всех элементов последовательности до 5го вычисляется по формуле:
(а(1)*(1-q^5))/(1-q)=(2*(1-243))/(1-3)=242
вычитаем из неё два известных элемента
242-2-162=78 - это и есть искомая сумма
ответ:78
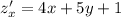
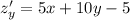
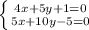
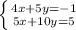
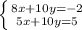
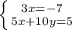
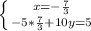
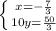
![H= \left[\begin{array}{cc}4&5\\5&10\end{array}\right]](/tpl/images/0857/3294/d1368.png)
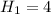
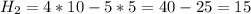
2 только. Возьмем сторону AD за x, тогда площадь треугольника AKD= 3*1/2x=18 чтобы избавиться от знаменателя, обе части домножаю на 2. В итоге: 6x=36 из этого х: 6