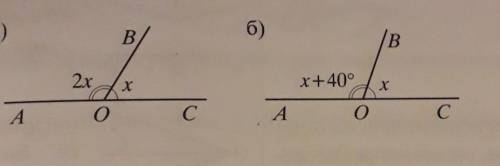
№ 39
17а - 13а = 4а
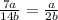
(11a *2) * 0.1 = 22a * 0.1 = 2.2a
48a : 12 = 4а
(9а * 8) : 3.6 = 72а : 3.6 = 20
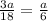
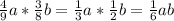
(1.3 * а) * 0.1 = 13а
12а + 10а - 9а = 13а
15а * 4 = 60а
16а : 0,4 = 40а
(7а * 4) : 0.5 = 28а : 0.5 = 56а
14а : 7 = 2а
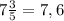
(7.6 * а) : 7.6 = а
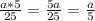
№40
3х +2х = 5х (при х=0)
5*0=0
7а - 2а = 5а (при а = 0,2)
5 * 0.2 = 1
28у - 7у = 21у (при у = 3)
21 * 3 = 63
15 + 6х + 2х = 8х + 15 (при х = 7)
8 * 7 + 15 = 56 + 15 = 71
45 + 27а - 3а = 24а + 45 (при а = 4)
24 * 4 + 45 = 96 + 45 = 141
32 + 21у - 8у = 32 + 13у (при у=6)
32 + 13 * 6 =32 + 78 = 110
11 - (2х+х) = 11 - 2х - х = 11 - 3х (при х = 2)
11 - 3 * 2 = 11 - 6 = 5
(10а - 8а) - 3 = 2а - 3 (при а = 5)
2 * 5 -3 = 10 - 3 = 7
4у + 5у = 9у (при у = 0,1)
9 * 0.1 = 0.9
35х + 4х = 39х (при х=4)
39 * 4 = 156
32а + 9а = 41а (при а = 7)
41 * 7 = 287
14 + 7у + 3у = 14 + 10у (при у = 5)
14 + 10 * 5 =14 + 50 = 64
27+12х-9х = 27 + 3х (при х = 4)
27 + 3 * 4 =39
39 + 15а - 12 = 27 + 15а (при а = 2)
27 + 15 *2 = 27 + 30 = 57
7+(5у-3у)=7+2у (при у = 1)
7+2*1=9
Пошаговое объяснение:а) Прямые АВ и А₁С₁ - скрещивающиеся, а расстоянием между скрещивающимися прямыми называют расстояние от некоторой точки скрещивающихся прямых (например точки А) к плоскости, проходящей через другую прямую плоскость треугольника АВС), параллельную первой прямой (АС), т.е это есть расстояние между АС и А₁₁С₁.. Оно равно боковому ребру АА₁, ч.т.д. б) 1) Обозначим угол между плоскостями АВС и АКС буквой α =45°. Построим угол α: проведём ВЕ⊥АС и КЕ⊥АС, тогда α= 45°. 2) Так как ВК : В₁К=2 : 3, то ВК=2х, В₁К=3х. 3) Рассмотрим ΔВЕК прямоугольный, т.к. =45°, то он равнобедренный,⇒ВК= ВЕ= 2х , ⇒ЕК²= (2х)²+(2х)²= 8х². 4) ΔАВС по условию равнобедренный, ⇒ АЕ=ЕС= АС/2 = 4√2 : 2= 2√2.Из ΔСЕК -прямоугольного ЕК²= КС² -ЕС² = 8² - (2√2)²= 64 - 8 = 56. 5) Но ЕК²= 8х², ⇒8х² =56, ⇒ х² = 56 :8 = 7, х=√7 6)Тогда искомое расстояние между прямыми АВ и А₁С₁: ВВ₁ =2х+3х=5х= 5·√7 Отв: ВВ₁ =5√7