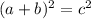
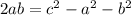- ещё раз возводим в квадрат: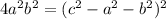
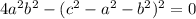
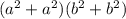, а второе слагаемое и разность получаются тривиально).
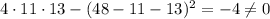, поэтому a, b, c гарантированно не удовлетворяют указанному равенству.
, 
, 
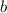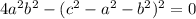выполняется но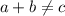 
. Решаем уравнение: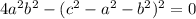
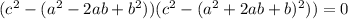
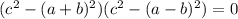
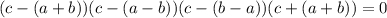
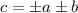(знаки выбираются независимо). Кроме нужного случая добавляются ещё 3 возможных решения, при этом два из них отсекаются при условии положительности чисел, остаётся только две возможности: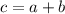
, 
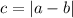
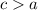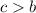, то реализуется первый случай, иначе - второй.
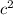- максимальное из трёх чисел.
номер 708
6. 17,5x=0,63
x=0,63÷17,5
x=0,036
9. 0,09x=94,5
x=94,5÷0,09
x=1050
номер 709
2. 7,91-6,72÷1,2=2, 31
4. 10,05+7,31÷1,7=14,35
6. 1,968÷0,41+28, 2=33