pq = 54
Пошаговое объяснение:
Пусть точки пересечения имеют вид 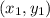 ,
, 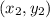 и
и  . Выразим через координаты то, что дано в условии.
. Выразим через координаты то, что дано в условии.
Сумма квадратов сторон:

(a - сумма квадратов, b - сумма попарных произведений)
Расстояние от начала координат до точки пересечения медиан
Известно, что координаты точки пересечения медиан можно найти по формулам:

Тогда квадрат расстояния от начала координат до точки пересечения медиан, для удобства умноженный на 9, выражается так:
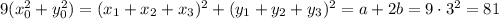
Получилась система линейных уравнений на a и b. Из неё 4b = 2 * 81 - 378 = -216, b = -54. Осталось выразить сумму попарных произведений, для этого понадобится немного преобразовать систему и вспомнить теорему Виета.
Умножаем уравнение параболы на x и заменяем xy на p, получается кубическое уравнение 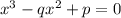 . Понятно, что найдя из этого уравнения x, потом по формуле y = p/x однозначно найдем y. Значит,
. Понятно, что найдя из этого уравнения x, потом по формуле y = p/x однозначно найдем y. Значит, 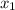 ,
, 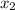 и
и 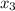 - корни кубического уравнения. По теореме Виета сумма их попарных произведений равна коэффициенту при x, он равен нулю.
- корни кубического уравнения. По теореме Виета сумма их попарных произведений равна коэффициенту при x, он равен нулю.
Умножаем уравнение параболы на 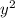 , избавляемся от x и получаем
, избавляемся от x и получаем 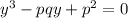 . Аналогично, нужна сумма попарных произведений, она равна -pq.
. Аналогично, нужна сумма попарных произведений, она равна -pq.
Приравниваем:

Острую форму лучевой болезни разделяют на четыре степени тяжести. К первой степени (легкой) относят величину облучения с дозой 1-2 Гр, она проявляется через 2-3 недели. Ко второй степени (средней тяжести) относят облучение с дозой 2-5 Гр, которая проявляется в течение пяти дней. К третьей степени облучения (тяжелой) относят полученную дозу в пределах 5-10 Гр, которая проявляет через 10-12 часов. К четвертой (крайне тяжелой) относят дозу облучения свыше 10 Гр, её проявление возможно через полчаса после облучения.
с вас лучший ответ ,не зря ведь я свою тетрадь по обж искала ))