S = 7×3×4×2=168см²
ответ: S=168см²
Вроде так:)
Задачка довольно не простая, поэтому решение будет длинным.
Просто хочу сказать что все что я решал до этого привело меня в полное безумие. И этим решением является текст данный мной ниже.
Так как гипотенуза равна 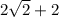 и один из катетов например AC = x, то катет AB =
и один из катетов например AC = x, то катет AB = 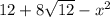
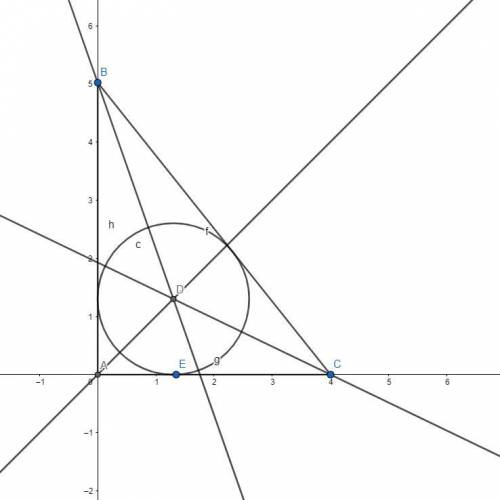
Проводим биссектрисы из двух остроугольных вершин.
Их пересечение создает треугольник ВDC:
Угол ∠ABC = 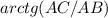
Значит ∠DBC = 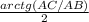
Угол ∠BCA = 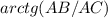
Значит ∠DCA = 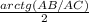 .
.
Напишем уравнение прямой BC
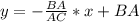
где BA = 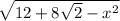 , AC = x
, AC = x
Теперь, зная что центр вписанной окружности находится на одинаковом расстоянии от сторон треугольника, напишем систему равенств.
Теперь ищем такое значение Dx, при котором Dx = расстоянию от точки D то прямой BC.
Расстояние от точки D то прямой BC будет равно по формуле
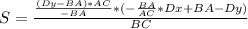
Составим систему равенств
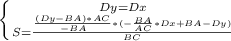
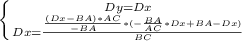
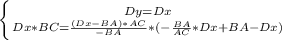
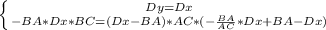
А теперь приступим к настоящему :
Так как гипотенуза равна 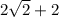 и один из катетов например AC = x, то катет AB =
и один из катетов например AC = x, то катет AB = 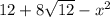
Проводим биссектрисы из прямой и остроугольной вершины.
Их пересечение создает треугольник ADC:
Угол ∠BAC = 90°
Значит ∠DAC = 45°
Угол ∠BCA = 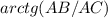
Значит ∠DCA = 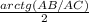 .
.
Найдем значение x1 при котором прямые AD и DC пересекаются:
x1 = 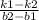 , где k1 и b1 коэффициенты прямой AD а k2 и b2 коэффициенты прямой DC.
, где k1 и b1 коэффициенты прямой AD а k2 и b2 коэффициенты прямой DC.
Площадь треугольника BDC равно 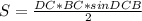 .
.
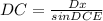
А радиус окружности равен 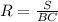
Подставим все известные нам величины.
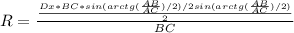
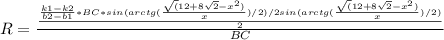
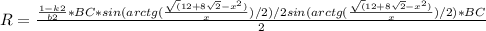
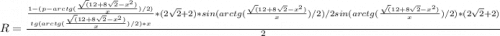 Получился полный капец.
Получился полный капец.
Я сам в шоке.
Я не просто в шоке, а в полном отчаянии, потому что нам сейчас надо найти производную от этого.
Самое обидное то, что я знаю какой будет ответ, а именно 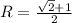
потому что максимальный радиус будет при равных катетах прямоугольного треугольника.
Но обоснование ответа будет мне стоить похоже 10 лет жизни.
прощения. Я не смог вам с решением данной задачи
ответ: 200 км.
Пошаговое объяснение:
Весь путь разделён на 3 части: 8/20, 7/20 и 50 км. То есть, кроме 50 км, у нас есть ещё
 пути.
пути.
Весь путь равен 20/20 (=1; мы поделили его на 20 частей, взяли все эти части и получился весь путь). Тогда 50 км составляют
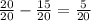
50 км = 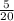 пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
пути. Разделим обе части равенства на 5 (и получим при этом верное равенство):
10 км =  пути.
пути.
Одна двадцатая часть — 10 км. Семь двадцатых частей в семь раз больше, чем одна двадцатая часть:
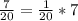
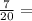 10 км * 7 = 70 км.
10 км * 7 = 70 км.
Восемь двадцатых частей в восемь раз больше, чем одна двадцатая часть:
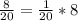
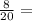 10 км * 8 = 80 км.
10 км * 8 = 80 км.
Обозначим весь путь за s. Тогда
s=I часть + II часть + III часть
s = 80 км + 70 км + 50 км = 200 км.
ответ: 200 км.
1) Если внимательно посмотреть на закрашенную фигуру, то увидим, что ее периметр НЕ ОТЛИЧАЕТСЯ от периметра исходного прямоугольника, часть сторон которого продолжена пунктиром.
Он имеет параметры:
длина a : 7+3 = 10 (м); ширина b: 4+2=6 (м).
(Стороны отрезанного угла нашей фигуры равны противоположным сторонам прямоугольника, вырезанного в исходном прямоугольнике, которые мы должны были бы учесть при подсчете периметра!).
Р = 2(a+b) = 2·(10+6) = 32 (м)
Для проверки подсчитаем периметр ЗАКРАШЕННОЙ фигуры по отрезкам сторон:
Р = 7+2+3+4+10+6 = 10+6+10+6 = 2·(10+6) = 2·16 =32(м)
2). Площадь закрашенной фигуры равна разности площадей большого и вырезанного прямоугольников:
S = a·b -a₁·b₁ = 10·6 - 3·2 = 60 - 6 = 54 (кв.м)
Можно подсчитать площадь закрашенной фигуры как сумму площадей двух прямоугольников, на которые мы можем ее мысленно разделить. Большого со сторонами 7 и 6 м, и маленького со сторонами 4 и 3 м
S = S₁ + S₂ = 7·6 + 4·3 = 42 + 12 = 54 (кв.см)
ответ: периметр закрашенной фигуры 32см, площадь 54 кв.см
Пошаговое объяснение: