Положение центра вписанной окружности определим, узнав высоту трапеции. Тогда r = 4/2 = 2. Окружность, описанная около трапеции, является одновременно и описанной около треугольника, стороны которого - диагональ, боковая сторона и большее основание. Диагональ равна: Радиус описанной окружности равен: Площадь треугольника равна: S = (1/2)*8*4 = 16 кв.ед. Тогда Так как центр описанной окружности лежит на оси симметрии трапеции. то определим его положение: H+Δ = √(R² - 1²) = √( 16.01563-1) = √ 15.01563 = 3.875. Отсюда Δ = 3.875 - 4 = -0,125. Значит, центр этой окружности лежит внутри контура трапеции - на 0,125 выше нижнего основания. ответ: расстояние между центрами вписанной и описанной окружностей равно 2-0,125 = 1,875.
1)1 2)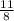
3)9 4)5
Пошаговое объяснение:
1) 3(4-x)+1=2(3-x)+6
12-3x+1=6-2x+6
-x=-1
x=1
2) (5-3x)-(7x-3)=-3-2x
5-3x-7x+3=-3-2x
-8x=-11
x=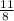
3) 2x-19=8-x
3x=27
x=9
4) 11-6x=31-10x
4x=20
x=5