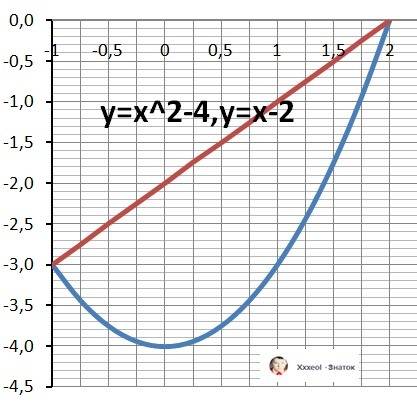
ДАНО: Y = x² - 4, Y = x - 2
НАЙТИ: Площадь фигуры.
РЕШЕНИЕ
Площадь фигуры - интеграл разности функций.
1. Находим пределы интегрирования - находим точки пересечения.
У1 =х² - 4 = У2 = х - 2
х² - х - 2 = 0 - решаем квадратное уравнение - это и есть разность функций.
b = - 1 - нижний предел, a = 2 - верхний предел.
2, Записываем разность функций - в обратном порядке и интегрируем.
s(x) = 2 - x - x² - интегрируем - находим первообразную.
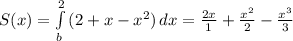
Лично мне нравится такая запись интеграла - понятно как получаются коэффициенты.
3. Вычисляем значения подставив пределы интегрирования.
S(2) = 4 +2 - 2 2/3 = 3 1/3 - подставили верхний предел
S(-1) = - 2 + 1/2 - 1/3 = - 1 1/6 - подставили нижний предел
S = S(2) - S(-1) = 3 1/3 - 1 1/6 = 4 1/2 = 4.5 - площадь - ОТВЕТ
Рисунок к задаче в приложении.
Данное арифметическое выражение обозначим через А = 101 + 102 + 103 + ... + 200.
В данной сумме 100 слагаемых.
Для вычисления данной суммы приемом Гаусса, сгруппируем попарно слагаемые, входящие в данную сумму так, чтобы эта парная группировка слагаемых дала каждой пары слагаемых одну и ту же сумму.
Заметим, что сумма каждой пары слагаемых, которые одинаково отстоят от концов данного выражения, равна 301:
101 + 200 = 301,
102 + 199 = 301,
103 + 198 = 301,
…и т. д ,
150 + 151 = 301
Нетрудно убедиться что таких пар, в 2 раза меньше, чем число слагаемых,
то есть 100 : 2 = 50.
значит А = 301 * 50 = 15050
ответ: А = 101 + 102 + 103 + ... + 200 =15050
1)-36/65
2)2/13
3)-13/3
4)-2/3
5)35/2
ну и так же можно сокращать, если надо сократишь. удачи)