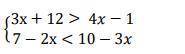
Так как грузовая машина ехала еще 4 часа после встречи то на пути она находилась 3+4=7 часов. Пусть скорость грузовой x а скорость легковой y. Тогда весьпуть будет равным 7x.Но с другой стороны когда они двигались навстречи друг другу то их скорость была равна x+y а путь равна 3(x+y) (так как они встретились черз 3 часа)
Значит 3(x+y)=7x => 3x+3y=7x => 3y=4x => y=4x/3. Тоесть скорость легковой машины 4/3 раза больше грузовой. Легковой машине оставалось пройти путь равный тому что грузовой до встречи тоесть 3x. Найдем время за кторорое он пройдет этот путь: 3x/y=3x:4x/3=9/4часа тоесть за 2ч15 минут
Поверни треугольник APB на 90o против часовой стрелки вокруг вершины B.
Будем считать, что AP = 1, BP = 2, CP = 3. Пусть P(1) — образ точки P при повороте на 90o против часовой стрелки вокруг вершины B. Тогда PBP(1) — равнобедренный прямоугольный треугольник. Поэтому уголBPP(1)= 45градусов, PP(1)=2 корня из 2. Следовательно PPв квадрате(1) + P(1)C в квадрате= 8+1=9=3 в квадрате=PC в квадрате.
Значит, треугольник PP(1)C — прямоугольный, угол PP(1) = 90градусов. Следовательно, угол APB = CP(1)B = угол CP(1)P + угол BP(1)P = 90градусов + 45градусов = 135грудусов.
ответ: 135 градусов.
Пошаговое объяснение:Нужно решить каждое неравенство системы в отдельности, а затем найти пересечение их решений.
Решим первое неравенство системы.
Решение первого неравенства системы
3
x
+
12
>
4
x
−
1
⇒
−
x
>
−
13
⇒
x
<
13
x
<
13
или
x
∈
(
−
∞
;
13
)
Из первого неравенства находим:
x
∈
(
−
∞
;
13
)
или
x
<
13
Решим второе неравенство системы.
Решение второго неравенства системы
−
2
x
+
7
<
−
3
x
+
10
⇒
x
<
3
x
<
3
или
x
∈
(
−
∞
;
3
)
Из второго неравенства находим:
x
∈
(
−
∞
;
3
)
или
x
<
3
Наносим найденные точки на числовую ось и вычисляем знаки на каждом интервале:
x
3
13
x
∈
(
−
∞
;
3
)
или
x
<
3