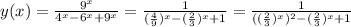
рассмотрим функцию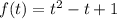 
, по свойствам ее минимальное значение достигается в вершине параболы (минимальное так как коэффициент при t равен a=1>0)
т.е. при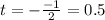 
далее рассмотрим функцию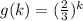 
-функция убывающая, поэтому чем меньше ее значение тем меньше ее значение
далее рассмотрим функцию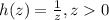 
- функция убывающая, чем меньше значение z тем большее значение h(z)
видим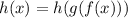 
учитывая непрерывность, и все ограничения, видим, что наибольшее значение данной функции достигается при
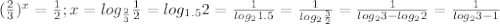
а наибольшее значение учитывая что для него выполняется соотношение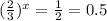 
будет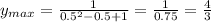 
1. Длина окружности L(окр) = 2*pi*R(окр) , длина сектора L(сект) = R(окр) *alpha.
Т. о. , периметр воронки L(вор) = L(окр) - L(сект)
2. R(воронки) = L(вор) /(2*pi)
высота воронки H(вор) = sqrt( R(окр) ^2 - R(воронки) ^2);
3. Имея функции R(вор) от alpha и H(вор) от alpha, имеем функцию для объема
V(вор) = pi*R(вор) ^2*H(вор) /3
Это функция от параметра alpha, берем производную, приравниваем к нулю, находя экстремум. Этот экстремум будет максимумом функции (минимумы - при alpha = 0 и alpha = 2*pi)
прости решать некогда