Это показательное уравнение вида , где неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения представить в виде числа со степенью так, чтобы в основании было число . Это явно число (проверка: ).
Значит теперь, когда наше показательное уравнение имеет вид , то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. .
Из этого следует, что ответ нашего показательного уравнения равен .
В слове "РАДИОСВЯЗЬ" 10 букв-цифр, ни одна из них не повторяется. Всего 10 цифр в математике: 0, 1, 2, 3,..9. Следовательно, эти цифры соответствуют буквам слова, значит произведение цифр числа "РАДИОСВЯЗЬ" равно 0: 0*1*2*...*9=0 - т.к. в произведении присутствует число 0.
Для решения под б): В+О+Д+А = 6 - разложим число 6 на сумму 4-х слагаемых. Возможен один вариант разложения: 0+1+2+3, все остальные варианты справедливы для меньшего числа слагаемых или для повторяющихся слагаемых.
Я+З+Ь = 24 - разложим число 24 на сумму трех слагаемых: 7+8+9 - это единственный вариант разложения.
Для букв Р, И, С остались следующие цифры: 4, 5, 6. Их сумма равна: Р+И+С=4+5+6=15
Это показательное уравнение вида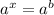
, где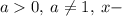 
неизвестная переменная.
Если сделаем основания степени равными, то по правилу сможем приравнять показатели степеней и решить обычное линейное уравнение.
Для этого, нужно член уравнения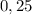
представить в виде числа со степенью так, чтобы в основании было число 
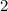. Это явно число 
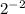(проверка: 
).
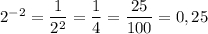Значит теперь, когда наше показательное уравнение имеет вид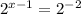
, то можем приравнять показатели степени и получим стандартное линейное уравнение. Решение этого уравнения и будет являться корнем исходного показательного уравнения.
Итак, мы получили уравнение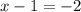
после того, как приравняли показатели степени. Решаем это уравнение. Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое. Т.е. 
.
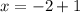Из этого следует, что ответ нашего показательного уравнения равен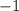
.
ответ: