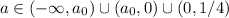, где 
Пошаговое объяснение:
В числителе стоит квадратный трёхчлен, у него может быть не более 2 корней. Значит, чтобы у уравнения было ровно 2 различных корня, числитель должен иметь 2 корня, и ни один из корней числителя не должен быть корнем знаменателя.
У числителя два неравных корня, если дискриминант больше нуля:
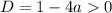
Найдём, при каких a хотя бы какой-то корень числителя является корнем знаменателя:
Подставляем найденный x в уравнение:
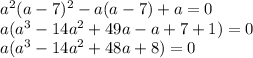
Один корень (a = 0) находится легко, еще один корень можно выписать по формулам для кубических уравнений или найти графически. Можно показать, что что этот корень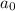 
единственный и удовлетворяет неравенству 1 - 4a > 0: производная функции 
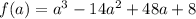равна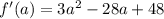 
. При a < 1/4 производная положительна, кроме того, 
, 
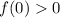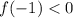, поэтому f(a) имеет корень на отрезке [-1, 0]. Выражение для 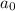довольно-таки громоздкое, по графику
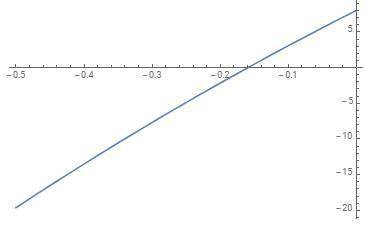
находишь производную.
она будет 8х-2х^3
потом приравнивает её к нулю
8х-2х^3=0
потом решаешь уравнение
х(8-2х^2)=0
х=0 или 8-2х^2=0
2х^2=8
х^2=4
х=+-2
то что мы нашли это точки, гед производная меняет знат с минуса на плюс, далее нужно построить координатную прямую, отметить на ней -2,0 и 2, а теперь числа, находящиеся между этими промежутками подставить в производную.
например после -2 стоит -3
подставим -3 в производную будет:
8*(-3)-2*(-3)^3=-24-2*-27=-24+54=30, число положительное, значит функция возрастает
теперь берём число между -2 и 0, подходит число -1. будет:
8*(-1)-2*(-1)^3=-8+2=-6, число отрицательное, функция убывает.
берём число 1:
8*1-2*1^3=8-2=6 число положительное, график возрастает.
возьмём число 3:
8*3-2*27=24-27=-3 теперь отметим на координатной прямой чередование знаков: рис(2)
получается, что от 1 вариант подходит, ответ 1