
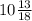
Пошаговое объяснение:
Прежде всего нужно перевести периодическую дробь в обыкновенную. В смешанных периодических дробях между запятой, отделяющей целую часть от дробной, и периодом могут присутствовать другие цифры. Смешанные периодические дроби следуют немного другим законам перевода в обыкновенные. Количество знаков в знаменателе остается равным количеству знаков после запятой, включая в период, но теперь знаменатель будет состоять не только из 9, но и из 0, где количество 9 – это количество цифр в периоде, а количество 0 – это количество цифр между запятой и периодом. Числитель же рассчитывается через разность числа записанного после запятой, включая период, и числа, представляющего набор цифр между запятой и периодом.
Целое число мы не трогаем, оставляем как есть, работаем только с дробью после запятой:
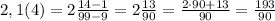
Итак, 20 процентов от некоего числа равны 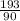
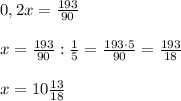
Пошаговое объяснение:
Квадратное уравнение имеет два корня тогда, когда его дискриминант больше нуля.
Найдем дискриминанты для каждого трёхчлена:
1) 4a^2 - 4b>0
2) 4a'^(2)-4b'>0
3) 4a''^(2)-4b''>0
Если произведение нечётного числа чисел больше нуля, то хотя бы один из них положительный, либо все три положительные.
Т.к. произведения равны, можем сказать, что её члены равны, но не известно в какой последовательности.
Допустим, что b<b'<b'', если наоборот, то всё равно будет также, но будет другой трёхчлен
Для начала предположим, что a=b, a'=b', a''=b'', тогда так как коэффициенты перед ними одинаковы, а а в квадрате, то получаем, что дискриминант каждого больше нуля, т.к. а больше b.
Теперь предположим, что a=b', a'=b, a''=b''
Теперь в первом случае а меньше b, и трёхчлен не будет иметь двух корней, но уже во втором случае a' больше b, тогда будет два корня, данное утверждение справедливо для всех перестановок
Для дифференцирования понадобится несколько формул:
\begin{gathered}\left( f(x) + g(x) \right)' = f'(x) + g'(x)left( n\cdot f(x) \right)' = n\cdot f'(x)left( x^n \right)' = n \cdot x^{x-1}\end{gathered}
(f(x)+g(x))
′
=f
′
(x)+g
′
(x)
(n⋅f(x))
′
=n⋅f
′
(x)
(x
n
)
′
=n⋅x
x−1
Исходное выражение удобно представить в виде:
F(x) = 3 \sqrt[3]{x^2} - x = 3 x^{2/3} - xF(x)=3
3
x
2
−x=3x
2/3
−x
Продифференцировав его, получаем:
\begin{gathered}F'(x) = (3 x^{2/3} - x)' = (3 x^{2/3})' - (x)' = 3 \cdot \dfrac{2}{3} \cdot x^{2/3 - 1} - 1 = 2\cdot x^{-1/3} - 1 = \dfrac{2}{\sqrt[3]{x}} - 1F'(1) = \dfrac{2}{\sqrt[3]{1}} - 1 = 2 - 1 = 1\end{gathered}
F
′
(x)=(3x
2/3
−x)
′
=(3x
2/3
)
′
−(x)
′
=3⋅
3
2
⋅x
2/3−1
−1=2⋅x
−1/3
−1=
3
x
2
−1
F
′
(1)=
3
1
2
−1=2−1=1