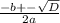. Например: х²-9х+8=0, D=(-9)²-4*1*8, D=81-32, D=49, x1=(9-√49)/2=(9-7)/2=2/2=1, x2=(9+√49)/2=(9+7)/2=16/2=8. Также есть неполные квадратные уравнения (без переменной с), решаются они выносом общего множителя за скобки. Например: 3х-х²=0, х(3-х)=0, х1=0, 3-х=0, х2=3; 3х²+х=0, х(3х+1)=0, х1=0, 3х+1=0, 3х=-1, х=-1/3; 4х²+20х=0, 4х(х+5)=0, 4х=0, х1=0, х+5=0, х=-5.
ну типо так?!
Пошаговое объяснение:
||2x – 4| – 5| = 9|+7| = 7
|-7| = 7,
поэтому, если |x| = 7, то делаем вывод, что x = +-7
A) |2x-5|-1 = 7 или |2x-5|-1 = -7
|2x-5| = 8 или |2x-5| = -6 ---это невозможно по определению модуля
2x-5 = 8 или 2x-5 = -8
2x = 13 или 2x = -3
x = 6.5 или x = -1.5
Б) |2x-1|-5 = 7 или |2x-1|-5 = -7
|2x-1| = 12 или |2x-1| = -2 ---это невозможно по определению модуля
2x-1 = 12 или 2x-1 = -12
2x = 13 или 2x = -11
x = 6.5 или x = -5.5
3x+2 = 5x+6 или 3x+2 = -(5x+6)
2x = -4 или 8x = -8
x = -2 или x = -1
в) (а-2х)²
Пошаговое объяснение:
Свойство четной (второй в частности) степени: знак числа при возведений в степень игнорируется. Например:
Это объясняется тем, что минус на минус дает плюс.
В нашем выражений можно вынести минус: