а) ..=59.52
б)=2,63
с)3,59
д)-91,5
е)58.
Відповідь:
1 та 2
Пояснення:
Розкладемо ліву частину нерівності на множники, розв'язавши відповідне квадратне рівняння:
-2x²+5x-2 = 0
2x²-5x+2 = 0
D = b²-4ac = (-5)²-4·2·2 = 25-16 = 9
x_1 = (-b+√D)/2a = (5+√9)/(2·2) = (5+3)/4 = 2
x_2 = (-b-√D)/2a = (5-√9)/(2·2) = (5-3)/4 = 0,5
Тоді -(2x²-5x+2) = -2(x-0,5)(x-2) = (2x-1)(2-x)
Тепер нерівність перетворена до такої: (2x-1)(2-x) ≥ 0
Розв'яжемо її методом інтервалів. Позначимо нулі функції в лівій частині нерівності (корені щойно розв'язаного рівняння) на числовій прямій та з'ясуємо знак цієї функції на кожному з проміжків, які утворяться (проставимо "+" або "-").
- + -
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯(0,5)¯¯¯¯¯¯¯¯¯¯¯¯¯¯(2)¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯
Множиною розв'язків буде проміжок, на якому функція набуває невід'ємних значень. Тобто x ∈ [0,5; 2]. Йому належать лише два цілих числа: 1 та 2.
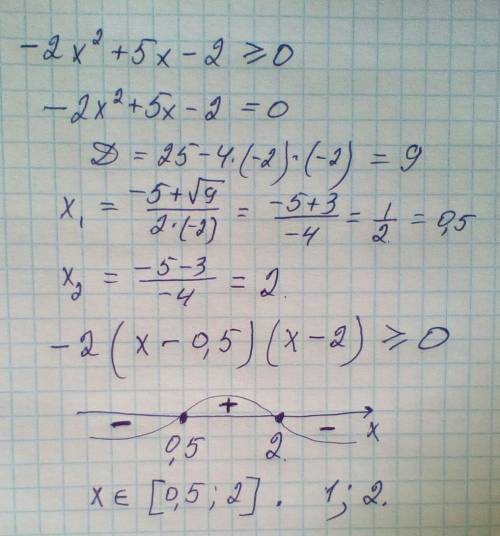
Дана функция f(х) на промежутке [0;Т], и заданы точки х0, x1, x2, нa этом промежутке. Требуется:
а) выписать ряд Фурье для функции f(x) в комплексной форме,
6) выписать вещественную форму ряда Фурье функции f(х),
в) построить график функции f(x)
и суммы ее ряда Фурье,
г) вычислить значение суммы ряда Фурье в заданных точках,
д) выписать ряд Фурье в амплитудно-фазовой форме,
е) построить амплитудный спектр ряда Фурье, вычислить А1, А2, А3, А4, А5,
ж) выписать равенство Парсеваля.
Дано:
f(x) = { -2, при 0 ≤ х < 2
{ х - 2, при 2 ≤ х ≤ 4
х0 = 2 , х1 = 2.5 , х2 = 4
Б) 2,63
В) 3,59
Г) -91,5
Д) 58