Решение Вашегозадания во вложении
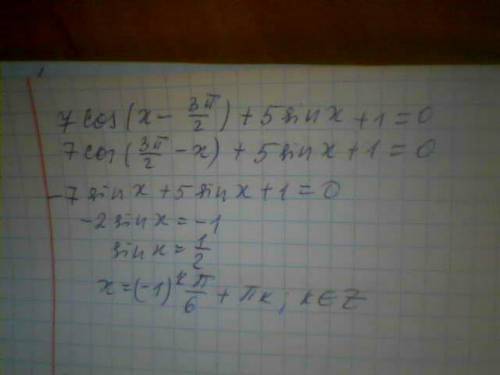
ответ:
пошаговое объяснение:
xy*dx+(1+y^2)*\sqrt{1+x^2}*dy=0|*\frac{1}{y\sqrt{1+x^2}}{xdx}{\sqrt{1+x^2}}=-\frac{(1+y^2)dy}{y} \frac{d(1+x^2)}{\sqrt{1+x^2}}=\int(-\frac{1}{y}-y){1+x^2}=-ln|y|-\frac{y^2}{2}+{1+x^2}+ln|y|+\frac{y^2}{2}={1+x^2}+ln|y|+\frac{y^2}{2})'=c'{x}{\sqrt{1+x^2}}+\frac{y'}{y}+yy'=0|*y\sqrt{1+x^2}dx\\xydx+(1+y^2)\sqrt{1+x^2}dy
в начале при делении потеряли ответ y=0, поэтому полный ответ:
(\sqrt{1+x^2}+ln|y|+\frac{y^2}{2}=c\ ; y=0
(1+x^2)*y'+y*\sqrt{1+x^2}=xy|*\frac{dx}{y(1+x^2)}{dy}{y}+\frac{dx}{\sqrt{1+x^2}}=\frac{xdx}{1+x^2}{dy}{y}=\frac{1}{2}\frac{d(1+x^2)}{1+x^2}-\frac{dx}{\sqrt{1+x^2}}{dy}{y}=\frac{1}{2}\int\frac{d(1+x^2)}{1+x^2}-\int\frac{dx}{\sqrt{1+x^2}}\\ln|y|=\frac{1}{2}ln|1+x^2|-ln|x+\sqrt{1+x^2}|+c\\ln|y|=ln|\sqrt{1+x^2}|-ln|x+\sqrt{1+x^2}|+ln|c|\\ln|y|=ln|\frac{c\sqrt{1+x^2}}{x+\sqrt{1+x^2}}|\\y=\frac{c\sqrt{1+x^2}}{x+\sqrt{1+x^2}}\\y*\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}=c
проверка:
(y*\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}})'=c'\\y'*\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}+y*{\frac{(1+\frac{x}{\sqrt{1+x^2}})*\sqrt{1+x^2}-\frac{x}{\sqrt{1+x^2}}*(x+\sqrt{1+x^2})}{1+x^2}}=0\\y'*\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}}+y*{\frac{(\frac{x+\sqrt{1+x^2}}{\sqrt{1+x^2}})*\sqrt{1+x^2}-\frac{x}{\sqrt{1+x^2}}*(x+\sqrt{1+x^2})}{1+x^2}}=0|*\frac{\sqrt{1+x^2}}{x+\sqrt{1+x^2}}\\y'+y\frac{\sqrt{1+x^2}-x}{1+x^2}=0|*(1++x^2)y'+y\sqrt{1+x^2}-xy=+x^2)y'+y\sqrt{1+x^2}=xy
в этом примере мы тоже теряем решение y=0, но дописывать его не надо т.к. у=0 при с=0
7cos(x-3pi/2) + 5sinx +1 = 0
По формулам приведения сos(x-3pi/2) = cos(3pi/2 - x) = -sinx
-7sinx +5sinx = -1
-2sinx = -1
sinx = 1/2
x = (-1)^n + pi*n, где х принадлежит Z.