Уравнение
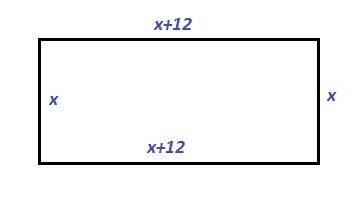
Пусть одна сторона прямоугольника равна х см.
Тогда вторая сторона равна х+12 см.
Периметр прямоугольника
Р = (x + x + 12) · 2 = 4x + 24
По условию периметр равен 1 м = 100 см.
4x + 24 = 100; 4x = 76; x = 19 см; x+12 = 19 + 12 = 31 см.
ответ: 19 см, 31 см.
=========================================
Стороны прямоугольника попарно равны. Периметр прямоугольника равен 1 м = 100 см. Тогда полупериметр прямоугольника (сумма двух не равных сторон) равна 100 : 2 = 50 см.
Известна сумма двух не равных сторон (50 см) и разность двух не равных сторон (12 см по условию).
По правилу решения задач на сумму и разность двух величин :
(50 - 12) : 2 = 19 см - меньшая сторона прямоугольника
19 + 12 = 31 см - большая сторона прямоугольника.
ответ: 19 см, 31 см.
ответ: а) 30, б) 3
Указание. Пусть в первом контейнере находится x коробок массой 19 кг и y коробок массой 49 кг. Тогда во втором контейнере находится соответственно 25-x и 19-y коробок. Тогда модуль разности суммарной массы можно записать: S=|19x+49y-((33-x)∙19+(27-y)∙49)| или S=2∙|19x+49y-975|.
a) Требование равенства количества коробок дает дополнительное условие x+y=30, поэтому выражение для модуля разности запишется S=2∙|19x+1470-49x-975|=
2*I495-30xI=30∙|33-2x|. Поскольку xϵZ, то минимальное значение модуля разности может быть сделано равным только единице |33-2x|>=1, поэтому ответ на п.а) 30.
б) Нужно найти количество коробок массы которых будут приблизительно одинаковыми:
49 кг * 2 кор.=98 кг
19 кг * 5 кор.=95 кг
98-95=3 кг
наименьшее значение S= 3