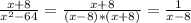
Искомое множество точек состоит из тех и только тех точек пространства, которые расположены на таком же расстоянии от прямой, как и точка 
.
Пусть 
является произвольным радиус-вектором точки на оси. Тогда искомое расстояние до прямой, очевидно, равно ![\rho=\frac{\left|[\vec{v},\; \vec{r}]\right|}{|\vec{v}|}](/tpl/images/1629/4338/88f2a.png)
, где 
есть направляющий вектор прямой, а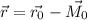 
.
Пусть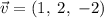 
. В качестве 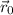можно взять 
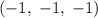при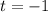 
.
![\left|[\vec{v},\; \vec{r}]\right| = \left|\det \left(\begin{array}{ccc}\textbf{i}&\textbf{j}&\textbf{k}\\1&2&-2\\-2&1&-2\end{array}\right)\right| = \sqrt{(-4+2)^2+(4+2)^2+(1+4)^2}=\sqrt{65}](/tpl/images/1629/4338/245f1.png)
,
;
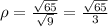Теперь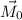 
можно заменить на произвольную точку 
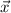. Тогда 
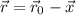. Уравнение примет вид: ![\frac{\sqrt{65}}{3} = \frac{\left|[\vec{v},\; \vec{r}]\right|}{3} \Rightarrow 65 = \left([\vec{v},\; \vec{r}]\right)^2](/tpl/images/1629/4338/b4dac.png)
. Распишем подробнее: ![\left([\vec{v},\; \vec{r}]\right)^2 = \left(\det\left(\begin{array}{ccc}\textbf{i}&\textbf{j}&\textbf{k}\\1&2&-2\\-1-x&-1-y&-1-z\end{array}\right) \right)^2=65](/tpl/images/1629/4338/387fa.png)
. Отсюда нетрудно получить окончательный результат: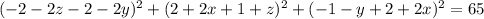 
, наконец 
.
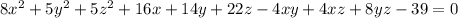(Возможно, есть некоторые арифметические ошибки, проверьте)
Зная длину стороны квадрата, можно найти его площадь: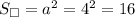 
см².
1) В этом квадрате проведены два полукруга. Мысленно доведём их до полных кругов. У каждого из них диаметр равен стороне квадрата, то есть, 4 см. Радиус же равен половине диаметра, то есть,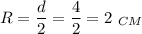 
. Площадь полукруга равна половине площади полного круга, получаем 
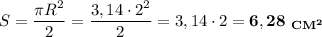. Таких полукругов в квадрате два. Чтобы найти площадь закрашенной голубым части, нужно из площади квадрата вычесть площади этих полукругов: 
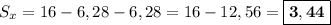см².
2) Всё то же самое, но полукруг уже один. Все данные мы вычислили в пункте и можем сразу найти искомую площадь: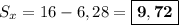 
см².
(X+8) \ (X^2 - 64) = (X+8) \ (X-8)*(X+8) = 1 \ X-8
ОТВЕТ: 1 \ Х-8