![b_3=b_1*q^2\\ b_6=b_1*q^5\\ \frac{b_6}{b_3}=\frac{b_1*q^5}{b_1*q^2}=q^3\\ q^3=\frac{625}{5}=125\\ q=\sqrt[3]{125}=5](/tpl/images/0172/6946/913f0.png)
Підставимо в формулу для b3 і знайдемо перший член прогресії:

Знайдемо суму перших 5 членів:

Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: 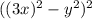 ; В следующих двух слагаемых вынесем общий множитель "40":
; В следующих двух слагаемых вынесем общий множитель "40":  ; В итоге получим следующее уравнение:
; В итоге получим следующее уравнение: 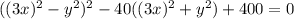 . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо
. В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо  будет стоять
будет стоять  ; Это приведет к тому, что придется убавить
; Это приведет к тому, что придется убавить 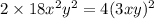 ; В итоге:
; В итоге: 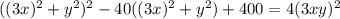 ; Слева стоит квадрат суммы. Уравнение примет вид:
; Слева стоит квадрат суммы. Уравнение примет вид:  ; Сворачивая еще раз:
; Сворачивая еще раз: 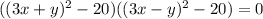 ; Получаем серию прямых:
; Получаем серию прямых:  ; А теперь приступим к рассмотрению первого уравнения.
; А теперь приступим к рассмотрению первого уравнения.
Это уравнение задает круг с центром в точке (0, 0) и радиусом  ; Рассмотрим прямую
; Рассмотрим прямую 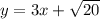 ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников.
; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 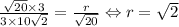 ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты
; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 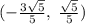 ; Ну а все решения:
; Ну а все решения:

Вероятность = Число "хороших" вариантов / Общее число вариантов
Общее число вариантов
Если в классе
1 ученик - 365 вариантов
2 ученика - 365^2 вариантов
( каждому варианту одного ученика соответствует каждый вариант другого )
...
23 ученика - 365^23 вариантов.
Найдем количество обратных вариантов - Что все дни рождения не совпадают.
Это число размещений 23 учеников по 365 местам
A(365;23) = 365! / (365-23)! = 365! / 342!
Вероятность обратного события
Q = 365! / 342! / 365^23
А нашего исходного
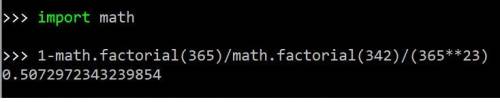
P = 1 - Q = 1 - 365! / 342! / 365^23
Тут увы без Питона не обойтись )))
На картинке !
Получилась вероятность даже больше чем 1/2
В половине классов из 23 учеников будут совпадающие Дни Рождения !
625/5=125
b1q^5/b1q^2=q^3
125=q^3
q=5
b1*25=5
b1=1/5
S=b1(5^5-1)/(5-1)=3124/20=156,2