Произведение всех делителей числа, не являющегося точным квадратом есть некоторый точный квадрат.
Так как у числа n 6 делителей, то есть четное число делителей, то оно не является точным квадратом.
Разложим число 432 на простые множители:
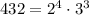
Таким образом, необходимо, чтобы шестой делитель имел в своем разложении на простые множители сомножитель 3 в нечетной степени.
Из предложенных чисел только число 12 удовлетворяет этому условию.
Действительно, в это случае произведение всех делителей будет являться точным квадратом:
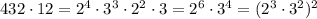
ответ: 12
Вопрос про бесконечность минус бесконечность очень важный. Если Вам дан обычный определенный (собственный) интеграл (интеграл Римана), функция обязана быть ограниченной (хотя этого может и не хватить для существования интеграла). Поэтому ни о какой бесконечности речи быть не может. Если интеграл понимается как несобственный, функция может быть и неограниченной, но если при вычислении предела от первообразной где-то получится бесконечность, интеграл сразу признается расходящимся. Но бывает еще интеграл в смысле главного значения - вот там бесконечности могут скушать друг друга.
Пример.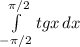 
. Как собственный интеграл он не существует (не существует конечный предел интегральных сумм, не зависящий от разбиения и выбора промежуточных точек), как несобственный интеграл он расходится, а в смысле главного значения равен нулю.
Постройте фигуру по координатам:
(2; 0).
(1; 1),
(2; 2),
(2; 1),
(3; 2),
(1; 4),
(0; 4),
(-1; 3,5),
(-1; 2,5),
(-1,5; 3),
(-2; 2,5),
(-1,5; 2),
(-2; 1,5),
(-1,5; 1),
(-1; 1),
(-0,5; 0),
(-1; -1),
(-1,5; -3),
(-2; -2,5),
(-2,5; -3),
(-2,5; -4),
(-2; -3,5),
(-1,5; -4),
(-1; -3),
(-1,5; -5),
(-2; -5,5),
(-2; -6),
(-1; -6),
(0; -4),
(1; -5),
(0; -6),
(1,5; -6),
(2; -5),
(2; -6),
(3; -6),
(3; -3),
(3; -5).
(2,5; -4),
(2,5; -3),
(1,5; -2),
(2:0).