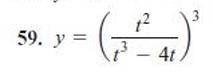
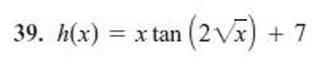
Пусть первоначально в 1 бочке было х л бензина, тогда во 2 бочке первоначально было (572-х)л бензина. Когда из первой бочки взяли 13л, в ней осталось (х-13)л, когда со 2 взяли 37 л в ней осталось (572-х-37)л. Известо, что когда из двух бочек взяли бензин, его количество в обеих бочкахстало одинаково. Имеем уравнение
х-13=572-х-37
х+х=572+13-37
2х=548
х=548:2
х= 274
Следовательно, первоначально в первой бочке было 274 л бензина, а во второй - (572-х)=(572-274)=298 л бензина
ответ: в первой бочке первоначально было 274 л бензина, во второй бочке первоначально было 298 л бензина.
Пошаговое объяснение: