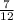Опустим из точки д перпендикуляр на авс. пусть это будет точка о. в треугольнике вдо проведём через точку е прямую, параллельную до. точку пересечения с плоскостью авс обозначим н. т. к. до перпендикулярно авс, а ен параллельно до, то ен перпендикулярно авс. поскольку угол между прямой и плоскостью - это угол между прямой и её проекцией на плоскость, то угол еан - искомый. как уже отмечалось, ен перпендикулярно авс, значит в частности ен перпендикулярно ан. т. о. треугольник аен прямоугольный с прямым углом н. тогда синус угла еан равен отношению ен к ае. обозначим сторону тетраэдра а. тогда ае=а*корень (3)/2, ао=2/3 ае=а*корень (3)/3, значит до=а*корень (6)/3, ен=1/2до=а*корень (6)/6. откуда синус еан=(а*корень (6)/6)/(а*корень (3)/2)=корень (2)/3.
Если наша площадь равна 36 см^2, а длина 9см, то ширина равна 4 см. Далее можно действовать двумя путями: 1) на обеих длинах отмерьте 3 см и поставьте точки, соедините. На обеих ширинах отмерьте 2 см, поставьте точки, соедините. Из получившихся 4 прямоугольников закрасьте 1 на выбор. 2) Проведите диагонали, то есть соедините противолежащие точки(те, что не лежат на одной стороне треугольника, например, длина - АВ, ширина - ВC. АС - будет диагональю). Всего должно быть две диагонали. Один из получившихся треугольников закрасьте.
Простые числа до 12: 2, 3, 5, 7, 11.
11 быть не может, иначе даже если брать минимальные из оставшихся чисел (2 и 3), получится 16 (16>12).
5 тоже не подойдет. Если еще одно простое 7 - третье просто не "влезет" в сумму. Остаются только 2, 3 и 7.
И правда, 2+3+7=12.
ответ: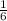 ,
, 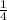 ,
,