S = a * b
1 сп.
Пусть х см - 1 сторона, тогда 2 сторона будет равна х - 44 см. По условию задачи площадь равна 675см².
Составим уравнение :
675 = х * ( x - 44 )
675 = x² - 44x
x² - 44x - 675 = 0
По теореме, противоположной теореме Виета:
x1 = 22 + √1159
x2 = 22 - √1159
2 сп.
Пусть х см - 2 сторона, тогда 1 сторона будет равна х + 44 см. По условию задачи площадь равна 675 см².
Составим уравнение:
675 = х * ( х + 44 )
675 = х² + 44х
х² + 44х - 675 = 0
По теореме, противоположной теореме Виета:
х1 = -22 + √1159
х2 = -22 - √1159 - корень отрицательный, что не может быть ( сторона не может быть отрицательной ), значит его мы не берём.
ответ: -22 + √1159 см
ответ: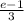
Пошаговое объяснение:
ответ: (e-1)/3
Пошаговое объяснение:
Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.
.
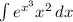Пусть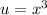 
, тогда ![x=\sqrt[3]{u}](/tpl/images/1117/3966/8c879.png)
.
![du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}](/tpl/images/1117/3966/82eee.png)
Делаем подстановку в наше изначальное выражение:
![\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }](/tpl/images/1117/3966/640b8.png)
Здесь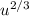 
сокращаются и мы имеем 
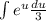. Выносим 
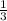за интеграл: 
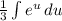. Теперь мы имеем знакомый интеграл, который равняется 
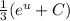, тоже самое что 
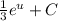. Подставляем 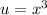и имеем 
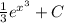. Используем фундаментальную теорему исчисления:
![\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}](/tpl/images/1117/3966/3089c.png)
косинус - прилегающего к гипотенузе
тангенс - противоположный к прилегающему катету
котангенс- прилегающий к противоположному