Посчитаем, сколько всего существует четырехзначных чисел.
Минимальное из них 1000, максимальное 9999.
9999 - 999 = 9000 чисел.
Найдем количество чисел, у которых в записи все цифры четные.
На первой позиции у них стоит цифра 2, 4, 6, 8 - 4 варианта выбора.
На второй, третьей и четвертой позициях - любая из 5 цифр: 0, 2, 4, 6, 8 - по 5 вариантов.
Всего комбинаций 4 * 5 * 5 * 5 = 20 * 25 = 500.
9000 - 500 = 8500 чисел.
ответ: Существует 8500 четырехзначных чисел, у которых хотя бы одна цифра в записи нечетная.
Пошаговое объяснение:
Прямая, которая задается уравнением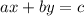 
, можно переписать в виде функции 
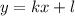, где 
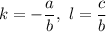
Коэффициент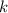 
отвечает за наклон прямой, равный тангенсу угла 
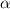, образованного данной прямой и положительным направлением оси 
, то есть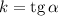 
Если 
, то график функции возрастает.
Если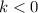 
, то график функции убывает.
Если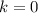 
, то график ни возрастает, ни убывает — имеем прямую 
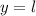, параллельную оси абсцисс.
а) Пусть прямая проходит через две точк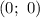и: 
и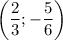 
Тогда, подставляя соответствующие координаты точек в функцию 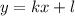, получим систему двух линейных уравнений:
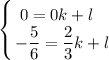
Тогда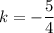 
и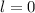 
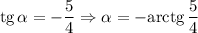— тупой угол наклона
Так как 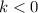, то график функции убывает.
б) Пусть прямая проходит через две точк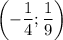и: 
и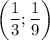 
. Тогда
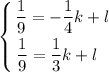
Тогда 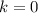и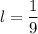 
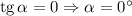
Так как 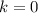, то график функции ни возрастает, ни убывает.
в) Пусть прямая проходит через две точки: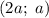 
и 
, где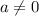 
— параметр. Тогда
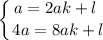
Умножим первое уравнение на 4 и получаем:
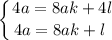
Тогда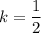 
и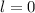
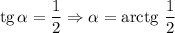— острый угол наклона
Так как , то график функции возрастает.
Переместительное св-во умножения. От перестановки множителей произведение не изменяется: а*ь=ь*а.
Сочетательное св-во сложения. Чтобы к сумме двух чисел прибавить третье число, можно к первому слагаемомуприбавить сумму второго и третьего: (а+ь)+с=а+(ь+с)
Свойства деления:
При делении числа на 1 получается само число: а:1=а
На 0 делить нельзя!
При делении числа, отличного от нуля, само на себя получаем 1 а:а=1
Деление суммы на число: (a + b) : c = a : c + b : c.
Деление разности на число: (a - b) : c = a : c - b : c.
Деление произведения на число: (a · b) : c = (a : c) · b = a · (b : c).