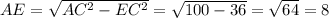 (см)
(см)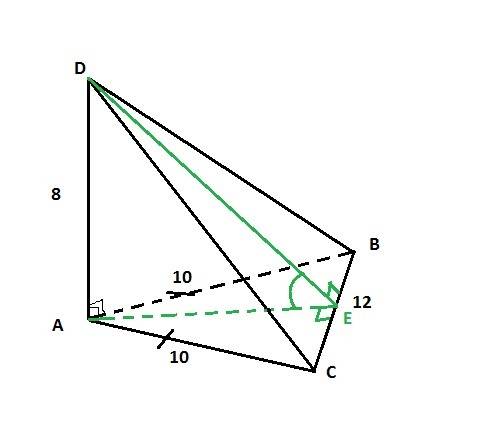
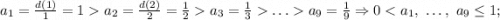
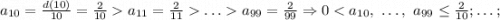
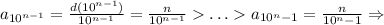
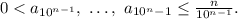
Последовательность 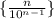 стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).
стремится к нулю, поэтому исходная последовательность стремится к нулю по лемме о "двух правоохранителях" (милиционерах, полицейских, жандармах, копах и т.д - в зависимости от страны и эпохи).
Доказать, что 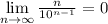 можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).
можно многими (с правила Лопиталя, теоремы Штольца, бинома Ньютона, неравенства Бернулли - кто подскажет еще ?).
Например, бином Ньютона дает нам следующую оценку:
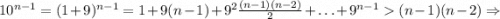
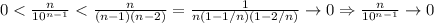 .
.
Неравенство Бернулли применяем так:
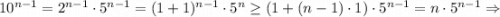
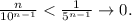
Лопиталь заменяет n на x, проверяет наличие неопределенности
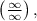 вычисляет предел отношения производных:
вычисляет предел отношения производных:
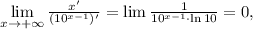 и поскольку предел отношения производных существует и равен нулю, исходный предел также равен нулю.
и поскольку предел отношения производных существует и равен нулю, исходный предел также равен нулю.
Штольц не так хорошо известен, но наш предел вычисляет мгновенно. Однако я устал и (возможно) утомил читателя. Поэтому, памятуя Козьму Пруткова, заканчиваю.
Перефразируем, когда автомобиль находился в точке О, мотоцикл отставал от него на 24км. Когда мотоцикл доехал до точки О, автомобиль был впереди него на 6км. Найти расстояние между точкой О и автомобилем в тот момент когда мотоциклист его догонит.
За время t1 мотоциклист проехал 24км, а автомобиль 6 км, значит скорость мотоциклиста в 4 раза больше скорости автомобиля. Если скорость автомобиля обозначить за икс, то скорость мотоциклиста будет 4x.
24 = t1 * 4x или 6 = t1 * x
Теперь представим что автомобиль не двигается, а скорость мотоцикла рассмотрим относительно него. Скорость мотоцикла в таком случае будет 3x.
Мотоцикл догонит автомобиль (проедет 6км) на скорости 3x за время t2
6 = t2 * 3x
Значит время t2 и t1 между собой связаны так: t1 = 3*t2
Подставим это выражение t1 в уравнение 6 = t1 * x :
6 = 3 * t2 * x или 2 = t2 * x
О чем нам это говорит - о том что за то время пока мотоцикл будет догонять автомобиль, автомобиль проедет 2км. А значит всего от точки О до автомобиля (и мотоцикла) будет 2+6 = 8км