Начерти квадрат со стороной 3 см
3×3=9 см² - площадь квадрата
Нехай дано циліндр, OO₁ - висота, α, β - площини основ.
γ - осьовий переріз.
AB = 6 см, AD = 8 см
Знайдемо S перерізу
Побудова
1) γ ∩ α = BC = 2R
γ ∩ β = AD = 2R
α║β
Отже, BC║AD (лінії перетину двох паралельних площин та третьої паралельні між собою)
2) BA║CD║OO₁ - висоти циліндра
OO₁ ⊥ β
Отже, BA ⊥ β, CD ⊥ β (якщо одна пряма перпендикулярна до іншої, то і всі прямі, що паралельні даній, теж перпендикулярні до іншої)
ABCD - осьовий переріз циліндра
Переріз побудовано
ABCD - паралелограм (протилежні сторони паралельні)
BA ⊥ β
AD ⊂ β
Отже, BA ⊥ AD (означення прямої, перпендиккулярної до площини)
∠ BAD = 90°, а, як наслідок, ABCD - прямокутник (паралелограм з кутом 90°)
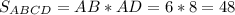 (см²)
(см²)
Відповідь: 48 см²
Так как в графе есть хотя бы одна вершина степени 5, есть хотя бы одна компонента с вершиной данной степени. Рассмотрим её. Кроме вершины степени 5 в этой компоненте не менее 5 вершин. Значит, в компоненте связности с вершиной степени 5 не менее шести вершин. Аналогично, в компоненте связности с вершиной степени 2 не менее трёх вершин. Значит, компонент не более 1 + (18 - 6) : 3 = 5.
Докажем, что любое количество компонент от 1 до 5 быть может. Сперва построим пример для 5 компонент. Пусть в одной компоненте две вершины степени 5 соединены ребром, а остальные вершины - вершины степени 2, присоединённые к обоим. Итого 6 вершин на одну компоненту. Остальные компоненты связности представлены циклами длины 3 из вершин степени 2.
Если требуется от 2 до 4 компонент, "склеим" две компоненты-цикла в одну, увеличив цикл.
Если требуется одна компонента, построим компоненту из шести вершин по примеру выше, а затем вместо ребра, соединяющего вершины степени 5, проложим путь из вершин степени 2.
ответ: От 1 до 5.
(P.S. Но это если граф обыкновенный, а в графе с петлями и кратными рёбрами можно устроить от 1 до 17 компонент.)
тобто кожна сторона квадрата 4 ми