Объем параллелепипеда равен 60 см³.
Пошаговое объяснение:
Требуется найти объем прямоугольного параллелепипеда, если известны площади трех граней.
Дано:
S передней грани = 25 см²
S боковой грани = 16 см²
S нижней грани = 9 см²
Найти: V.
Обозначим длину, ширину и высоту параллелепипеда соответственно a, b, h.
Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.Вспомним:
Площадь прямоугольника равна произведению смежных сторон.1. Рассмотрим данный параллелепипед.
Объем параллелепипеда равен произведению площади основания на высоту.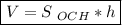
Основание - это нижняя грань.
Значит площадь основания 9 см².
Теперь найдем высоту.
2. Из формулы площади передней грани выразим a:
S пг = аh
25 = аh
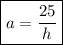
3. Из формулы площади боковой грани выразим b:
S бг = bh
16 = bh
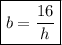
4. В формулу площади нижней грани подставим выше найденные значения а и b и найдем h:
S нг = аb
9 = ab
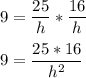
Воспользуемся основным свойством пропорции:
Произведение средних членов равно произведению крайних.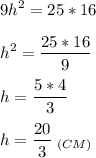
5. Найдем объем параллелерипеда.
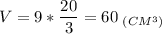
Объем параллелепипеда равен 60 см³.
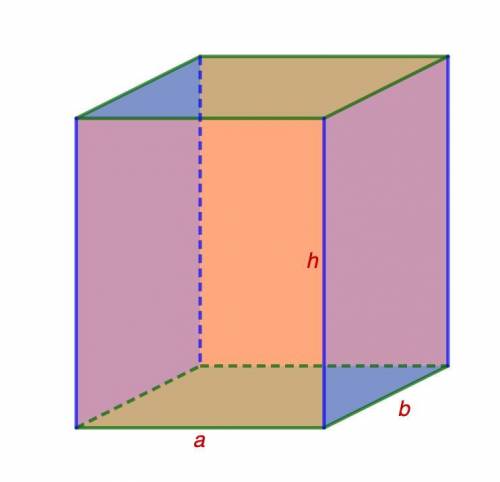
1) s₁=12 дм²=12*0,01 м²=0.12 м²; s₂=120 см²=120*0,0001 м²=0,012 м²;
s₁/s₂=0,12/0,012=10.
2) s₁=25 м²; s₂=1300 дм²=1300*0,01 м²=13 м²;
s₁/s₂=25/13=1,92.
3) s₁=32 га=32*10 000 м²=320 000 м²; s₂=32 10⁶ м²=32 000 000 м²;
s₁/s₂=320 000/32 000 000=0,01.
4) s₁=5 10³ м²=5 000 м²; s₂=50 000 мм²=50 000*0,000 001 м²=0,05 м²;
s₁/s₂=5000/0,05==100 000.
1) V₁=16,5 дм³=16,5*0,001 м³=0,0165 м³; V₂=0,165 м³
V₁/V₂=0,1.
2) V₁=82 мл=82 см³; V₂=82 cм³;
V₁/V₂=1.
3) V₁=4 л=4 дм³=0,004 м³; V₂=3255 cм³=0.003255 м³;
V₁/V₂=0,004/0,003255=1,23.
4) V₁=1 10³ дм³=1000*0,001 м³=1 м³; V₂=248,5 мм³=0,0002485 м³;
V₁/V₂=4024.
Подробнее - на -
Если пятая часть числа - пятая степень, то 2 и 3 входят в разложение в степени, кратной 5, а 5 входит в степени, дающей при делении на 5 остаток 1.
Если третья часть - куб, то 2 и 5 входят в разложение в степени, кратной 3, а 3 входит в степени, дающей при делении на 3 остаток 1.
Если половина - квадрат, то 3 и 5 входят в разложение в четной степени, а 2 - в нечетной.
Итак, 2 входит в степени, кратной 3, 5 и притом в нечетной. Т.к. нужно найти наименьшее число, то 2 входит в 15 степени.
Аналогично, 3 входит в степени, кратной 2 и 5, притом дает в остатке при делении на 3 остаток 1. Наименьший показатель степени, подходящий под эти условия, это 10.
Показатель у 5 отвечает требованиям: делится на 2 и 3, дает при делении на 5 остаток 1. Подходит 6.
Искомое число равно