вот держи думаю что правильно. деятель бунин.
бунин иван алексеевич (1870-1953). писатель. из обедневшей дворянской семьи. в молодости работал корректором, статистиком, библиотекарем, репортером. печатался с 1887 г.
первые книги и. бунина - стихотворные сборники. стихи его - пример «старой» классической формы. тема поэзии молодого бунина - родная природа. тогда же он начал писать рассказы. в 1899 г. и. бунин начинает сотрудничать с издательством «знание». лучшие рассказы этого периода - «антоновские яблоки» (1900), «сосны» (1901), «чернозем» (1904). серьезный общественный резонанс имела повесть «деревня» (1910). хроникой вырождения усадебного дворянства стала повесть «суходол» (1911). проза и. бунина - образец живописности, строгости, ритмической выразительности.
поэтический сборник и. бунина «листопад» (1901 г.) - получил пушкинскую премию. в 1909 г. бунин избирается почетным академиком. прославился перевод буниным поэмы лонгфелло «песня о гайавате». в 1920 г. бунин эмигрирует. в дальнейшем он живет и работает во франции.
в эмиграции он создает произведения о любви («митина любовь», 1925 г.; «дело корнета елагина», 1927 г.; цикл новелл «темные аллеи» 1943 центральное место в творчестве позднего бунина занимает автобиографический роман «жизнь арсеньева» (1930 в 1933 г. писателю была присуждена нобелевская премия. за рубежом и. бунин создал также философско- трактат о толстой л.н.л.н. толстом «освобождение толстого» (1937 г.) и «воспоминания» (1950
7
Пошаговое объяснение:
1) Думаю самое быстрое решение - это графический метод:
строим графики функций по точкам
![y=\sqrt[3]{4x-1} \\ y=\sqrt[3]{x+1} +1](/tpl/images/1177/9847/7d0e9.png)
они пересекаются в точке с абсциссой x=7, что и будет ответом.
2) Но если нужно аналитическое решение, то вот одно из них
сделаем замену:
![\sqrt[3]{x+1} =t](/tpl/images/1177/9847/6528e.png)
тогда
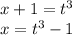
имеем уравнение:
![\sqrt[3]{4(t^3-1)-1} -t=1 \\ \\ \sqrt[3]{4t^3-5} =t+1](/tpl/images/1177/9847/49dbb.png)
возводим обе части в куб:
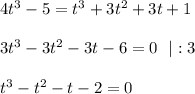
если данное уравнение имеет целые корни, то они среди делителей свободного члена (-2)
То есть возможные корни: ±1; ±2
перебирая их, выясняем, что подходит только t=2.
Действительно, 2³-2²-2-2=0
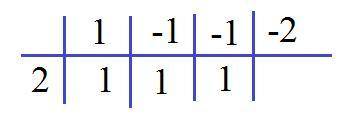
Далее понижаем степень уравнения, например, по схеме Горнера (см. рисунок)
t²+t+1=0
D=1-4=-3<0 ⇒ корней нет
Получается единственный корень t=2
Обратная замена: ∛(x+1)=t
![\sqrt[3]{x+1}=2 \\ \\ (\sqrt[3]{x+1})^3=2^3 \\ \\ x+1=8 \\ \\ x=7](/tpl/images/1177/9847/fbddb.png)
2cosx=√3 | :2
cosx=√3/2
x=+-arccos(√3/2)+2Пn; n∈Z
x=+-П/6+2Пn; n∈Z.