4
Пошаговое объяснение:
Оба уравнения в системе задают окружности. Первое уравнение - окружность с центром в точке О и радиусом 4. Параметр а во втором уравнении при увеличении значения двигается окружность по оси Х вправо, при уменьшении влево соответсвенно. Если a = 0, имеем уравнение x^2+y^2=1 (окружность с центром в т. О и радиусом 1). Система при этом не будет иметь решений (окружности не пересекаются). Одно решение система имеет при а = ±3 и а=±5. Два решения при -5<a<-3 и 3<a<5. Наибольшим целым а тогда будет 4.
Здравствуйте!
Есть такие примеры!
6853...9
+ 2...4...3...
_________
...90257
Смотрим с конца. 9+х=7. Получаем отрицательное число. Такое невозможно. Значит мы должны прибавить десять к 7. 17. 9+х=17; х=8.
Ставим 8, но не забывает прибавить 1 к десяткам, который мы сделали.
6853...9
+ 2...4...38
_________
...90257
1+х+3=5; 4+х=5; х=1.
685319
+ 2...4...38
_________
...90257
3+х=2; отриц. число, прибавляем десяток; 3+х=12; х=9
685319
+ 2..4938
______
..90257
5+4+1=10, т.е. на след. десяток ещё 1 прибавляем.
685319
+ 2..4938
______
..90257
1+8+х=9; х=0
685319
+ 204938
______
..90257
6+2=х; х=8.
685319
+ 204938
______
890257
Сверяем. При сложении получаем сумму, которая нужна.
В вычитании всё тоже самое.
803...0
- 1253...
_______
6...764
0-х=4, отрицательное число, значит нужно прибавить десяток, а из "соседнего левого вычитания" вычесть 1. 10-х=4; х=6.
803...0
- 12536
_______
6...764
х-3-1=6; х-4=6; х=10, но занимаем из левого вычитания 1.
80300
- 12536
_______
6...764
2 (3-1) -5 не равно 7. Значит 12-5=7, занимаем
80300
- 12536
_______
6...764
0-1-2 получится отрицательное число. Значит занимаем. 10-1-2= 7
80300
- 12536
_______
67764
Проверяем. Всё сходится!
В итоге получаем примеры:

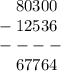
Пусть у Коли было х монет, а у Сережи у монет.
Тогда вмесье у них было
х+ у =60
После того как Коля отдел Сереже 5 монет у него стало х-5 а у Сережи у+5
Так как у Коли стало в 2 раза больше чем у Сережи то можно записать
x-5 =2(y+2)
Запишем систему уравнений
{x+y=60
{ x-5 =2(y+5)
Решим систему уравнений методом подстановки
Из первого уравнения найдем х и подставим во второе уравнение
х+у=60 или х =60-у
x-5 =2y+10
60-y-5 = 2y+10
3y = 55-10
y =45/3
y=15
x=60-15 =45
Проверка
х+у =15+45 =60
x-5 =2(y+5)
45-5 =2(15+5)
40=40
Поэтому у Коли было 45 монет у Сережи было 15 монет
ответ:45;15