Пошаговое объяснение:
1) скорость катера 18км/ч, скорость реки 3км/ч. По течению 18+3=21 км/ч, против течения 18-3=15 км/ч. 2). По течению скорость лодки будет 48÷3=16км/ч, против течения 48÷4=12 км/ч
1. Собственная скорость лодки равна х км в час.
2. Скорость течения реки равна y км в час.
3. Составим первое уравнение, если известно что скорость лодки по течению равна 16 км в час.
x + y = 16;
4. Выразим из него y, y = 16 - х.
5. Составим второе уравнение, если известно что скорость лодки против течения равна 12 км в час.
х - y = 12;
6. Подставим во второе уравнение выраженный из первого уравнения y. Найдем скорость лодки.
х - (16 - х) = 12;
х - 16 + х = 12;
2х = 12 + 16;
2х = 28;
х = 28 / 2;
х = 14 км в час.
7. Найдем скорость течения реки.
y = 16 - 14;
y = 2 км в час. 3). Скорость катера 15км/ч, а скорость реки 3 км/ч, следовательно по течению 15+3=18км/ч. 15-3=12км/ч против течения. 54÷18=3 часа время в пути по течению. 54÷12=4,5 часа против течения. 3+4,5=7,5 часов потребуется катера на путь туда и обратно.
Пусть первая труба пропускает
литров. Тогда вторая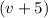 
л. Если мы вычтем из более производительной трубы мене производительную, то получим время, которое требуется второй трубе, когда первая труба уже заполнила резервуар. Это время по условию равно 10 мин:
Второй корень явно отрицателен, поэтому он нам не подходит, т. к. скорость/производительность — величина положительная.
Тогда вторая труба по условию пропускает 10+5=15 л/мин
ответ: 1-я труба — 10 л/мин, 2-я труба — 15 л/мин.
Проверка: первая труба заполнит первый резервуар за 150:10=15 мин.
Вторая труба за 75:15=5 мин. Мы видим, что первый резервуар заполняется на 10 минут дольше, что и требовалось доказать.