. Упростите выражение и выпишите коэффициент: 1) -0, la . (-10b); 3) -0,7с. 0,4d;
2) 1,2а . (-b) . 0,5с; 4) 5cd . (-0,2);
Выражения:
5) -1,6xy - (-0,5);
6) 0,18a - (-105)
ОТДАЮ

Question

Математика: . Упростите выражение и выпишите коэффициент: 1) -0, la . (-10b); 3) -0,7с. 0,4d; 2) 1,2а . (-b) . 0,5с; 4) 5cd . (-0,2); Выражения: 5) -1,6xy - (-0,5); 6) 0,18a - (-105) ОТДАЮ​

Artem0405 · Accepted Answer

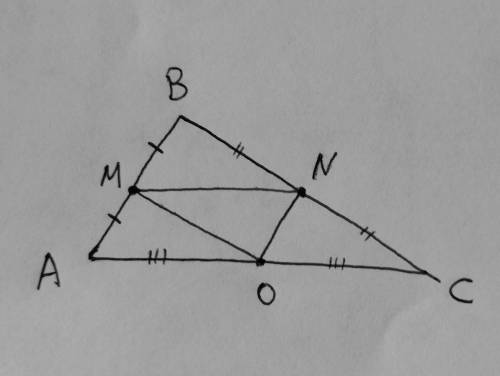
Дано:стороны треугольника соотносятся как 2:3:4P(MNO) = 27 смНайти: стороны треугольникаПо свойству средней линии треугольника, три средние линии делят исходный треугольник на четыре равных треугольника. Треугольник MNO — серединный. По свойству серединного треугольника следует, что P(MNO) = (P(ABC)) / 2Пусть стороны треугольника будут 2х, 3х, 4х соответсвенно. AB = 2x, BC = 3x, AC = 4xP(ABC) = AB + BC + AC = 2x + 3x + 4x = 9xДано, что P(MNO) = 27 см, значит27 = (9х) / 29х = 54х = 6, отсюда следует,...

. Упростите выражение и выпишите коэффициент: 1) -0, la . (-10b); 3) -0,7с. 0,4d;2) 1,2а . (-b) . 0,5с; 4) 5cd . (-0,2);Выражения:5) -1,6xy - (-0,5);6) 0,18a - (-105) ОТДАЮ​

MOGZ ответил

. Упростите выражение и выпишите коэффициент: 1) -0, la . (-10b); 3) -0,7с. 0,4d;
2) 1,2а . (-b) . 0,5с; 4) 5cd . (-0,2);
Выражения:
5) -1,6xy - (-0,5);
6) 0,18a - (-105)
ОТДАЮ