20 - дневная производительность труда мастера до начала соревнования;
24 - дневная производительность труда мастера в ходе соревнования;
10 - дневная производительность ученика до начала соревнования;
11 - дневная производительность ученика в ходе соревнования.
Пошаговое объяснение:
Пусть первоначальная дневная производительность труда мастера равна х, а первоначальная дневная производительность одного ученика равна у.
Тогда можно составить следующую систему уравнений:
(5х + 7у) · 5 = 850 (1)
(5х · 1,2 + 7у · 1,1) · 5 = 985 (2)
или
5х + 7у = 170 (3)
6х + 7,7 у = 197 (4)
Умножим уравнение (3) на 1,1:
5,5 х + 7,7 у = 187 (5)
и из уравнение (4) вычтем уравнение (5):
6х - 5,5х + 7,7у - 7,7у = 197 - 187
0,5х = 10
х = 20 - дневная производительность труда мастера до начала соревнования;
20 · 1,2 = 24 - дневная производительность труда мастера в ходе соревнования.
Подставим х = 20 в уравнение (3):
5 · 20 + 7у = 170
7у = 170 - 100 = 70
у = 70/7 = 10 - дневная производительность ученика до начала соревнования;
10· 1,1 = 11 - дневная производительность ученика в ходе соревнования.
ПРОВЕРКА
(5 · 20 + 7 · 10) · 5 = 850
(5 · 24 + 7 · 11) · 5 = 985
20 - дневная производительность труда мастера до начала соревнования;
24 - дневная производительность труда мастера в ходе соревнования;
10 - дневная производительность ученика до начала соревнования;
11 - дневная производительность ученика в ходе соревнования.
ответ: a) 0,3456
б) 0,68256
в) 0,92224
Пошаговое объяснение:
При решении используется формула Бернулли.
Вероятность вытянуть изделие высшего сорта p = 40% = 0,4
Вероятность не вытянуть изделие высшего сорта q = 1 - p = 1 - 0,4 = 0,6
а) A: "из пяти случайно отобранных изделий 2 высшего сорта"
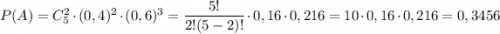
б) B: "из пяти случайно отобранных изделий не более 2 высшего сорта"
Не более двух - это 0, 1 или 2 изделия высшего сорта
C: "из пяти случайно отобранных изделий 1 высшего сорта"
D: "из пяти случайно отобранных изделий 0 высшего сорта"
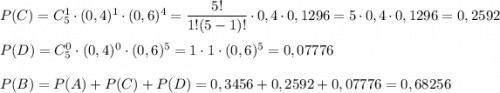
в) E: "из пяти случайно отобранных изделий хотя бы одно высшего сорта"
Найдём вероятность события E через противоположное событие D.
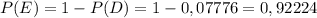
156. надеюсь кому-то