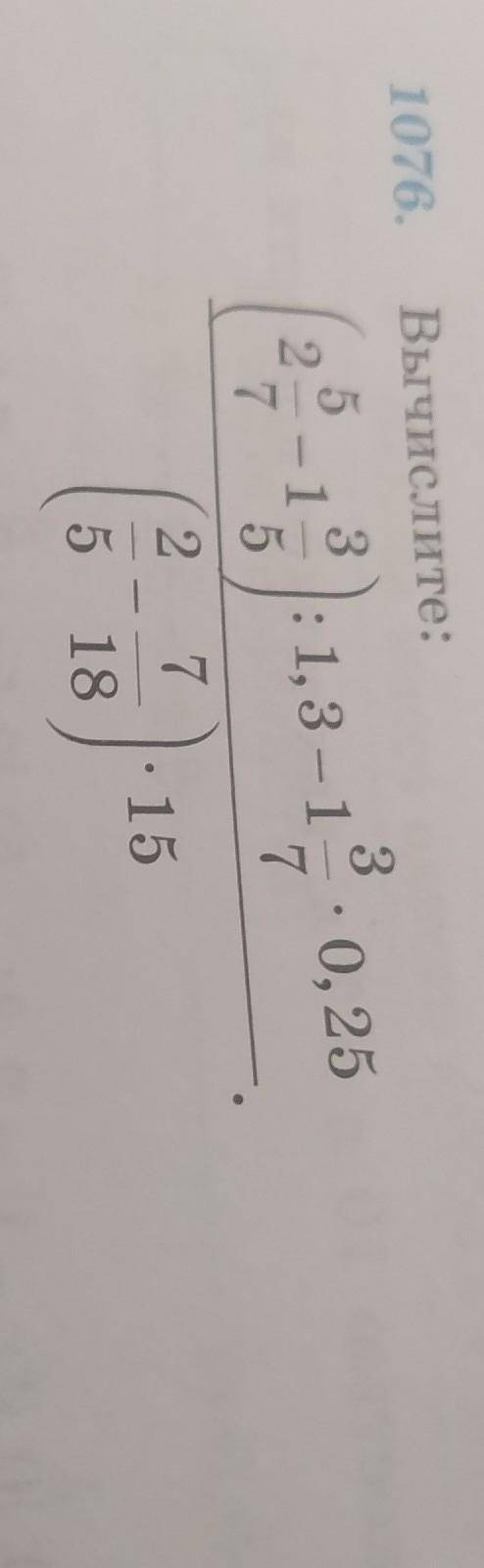
Непонятно условие: первую треть пути или первую треть времени?
Так лучше.
Итак, пусть скорость первого участка V. Второго V-3
Время на первом участке Т, на втором - 2Т.
Общее расстояние равно VT +2T(V-3) = 3VT - 6T = 3T(V-2)
Средняя скорость - это всё расстояние/время в пути = 3T(V-2) / (Т+2Т) = (V-2). По условию средняя скорость равна 17. Значит, V = 19. Это на первом участке. На втором, значит, 16.
или
В подобных задачах оперируют обычно величинами обратными скорости, т.е. временем. Расстояние вычисляется по формуле: S=v*t. Нам нужно время: t=S/v. Теперь перейдем к задаче. Дорога состоит из 2 частей S1=1/3*S и S2=2/3*S. Затраченное время, с одной стороны t=S/v, с другой стороны t=S1/v1+S2/v2. Приравняем и подставим данные:
Уравнение:
36/x-36/(x+3)=1
36(x+3)-36x=x(x+3)
36x+108-36x=x^{2}+3x
x^2+3x-108=0
D=9+4*108=441=21^2
x1=(-3+21)/2=9
x2=(-3-21)/2=-12<0 не подходит
2) 9+3=12(км/ч)
ответ: Скорость первого велосипедиста равна9 км/ч, а второго-12 км/ч.
вот вроде бы так , это приложение всегда правильно решает (у меня точно)