22 дня
Пошаговое объяснение:
Задание
Первая бригада может покрасить забор за 18 дней, а вторая за 24 дня. Первая бригада работала над выполнением этого задания 6 дней, после чего вторая бригада закончила работу. За сколько всего дней было выполнено задание?
Решение
1) Рассчитаем, какую часть задания выполнила первая бригада:
6 : 18 = 1/3.
2) Следовательно, второй бригады надо было выполнить оставшуюся часть задания, что составляет:
1 - 1/3 = 2/3 всей работы.
3) Второй бригаде для выполнения всей работы потребовалось бы 24 дня. Рассчитаем, сколько дней необходимо второй бригаде для того, чтобы выполнить оставшиеся 2/3 задания:
24 · (2/3) = 48 : 3 = 16 дней.
4) Всю работу выполняли:
первая бригада - в течение 6 дней,
вторая бригада - в течение 16 дней.
Следовательно, всё задание было выполнено за:
6 + 16 = 22 дня.
ответ: всё задание было выполнено за 22 дня
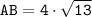 (ед)
(ед)
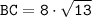 (ед.)
(ед.)
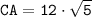 (ед.)
(ед.)
Пошаговое объяснение:
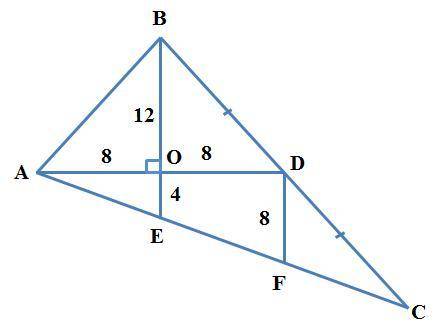
Дано (см. рисунок):
ΔABC
BE - биссектриса
AD - медиана
BE⊥AD
BE=AD=16 (ед.)
Найти AB, BC, CA.
Решение.
Пусть O точка пересечений биссектрисы BE и медианы AD. По условию BE⊥AD, откуда следует что BO биссектриса и высота, следовательно, треугольник ABD равнобедренный: AB=BD и BO медиана. Отсюда
AO=OD=AD/2=16/2=8.
Проведём DF так, чтобы DF║BE. Так как AD медиана, то BD=DC, следовательно DF средняя линия в треугольнике BEC. Отсюда, по свойству средней линии
DF=BE/2=16/2=8.
По построению OE║FD. Так как BO медиана, то AO=OD, следовательно OE средняя линия в треугольнике ADF. Отсюда, по свойству средней линии
OE=DF/2=8/2=4.
По условию BE⊥AD, что и OE⊥AD. Тогда треугольник AOE прямоугольный с гипотенузой AE. Применим теорему Пифагора:
AE²=AO²+OE²=8²+4²=64+16=80=4²·5,
откуда 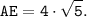
По условию BE - биссектриса и по свойству биссектрисы
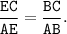
Как отметили ранее, AB=BD=BC/2 и BD=DC, то есть BC=2·AB. Поэтому
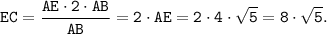
Теперь можем найти
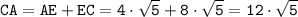 (ед.).
(ед.).
Используя OE=4 находим
BO=BE-OE=16-4=12.
Так как BE⊥AD, то треугольник AOB прямоугольный с гипотенузой AB. Применим теорему Пифагора:
AB²=AO²+OB²=8²+12²=64+144=208=4²·13,
откуда
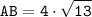 (ед).
(ед).
Из AB=BC/2 находим:
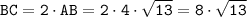 (ед.).
(ед.).
Различаются порядком расположения цифр по разрядам, т.е. они неравны друг другу ни один.
2. Можно на подобии этого составить: 123456,132456,213456,231456,312456,321456.
3. 123456+132456=255912
123456+231456=354912
231456+312456=543912
312456-123456=189000
231456-123456=108000
321456-123456=198000
4. Не совсем понятна фраза "Выбери из чисел такое,при умножении которого на однозначные числа,больше на 1,получаются шестизначные числа."
Предполагаю только, что надо из перечисленных выше чисел выбрать такое, что если к нему прибавить 1 и умножить результат на однозначное число получится шестизначное.
В перечисленных таких чисел нет. мы можем некоторые из них умножить на 2,3,4,5,6 и результат получится шестизначным, но если умножить на 9, то итог будет больше.
Подходящее число нам может быть, например:
111110.
Прибавим к нему единицу = 111111
Умножим на 9 = 999999 шестизначное.