
иррациональные цисла - действительные не являющиеся рациональными...
доказать существование - достаточно привести пример.
Пример иррационального числа 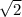
понятно, что оно действительное (величина длины диагонали квадрата со стороной 1, например), покажем, что оно не является рациональным, то есть не существует дроби х/у=√2, где х - целое, у - натуральное
Предположим обратное, то есть такие х и у существуют, тогда
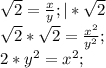
(самое сложное)
разложив на множители х и у получим:
слева в равенстве число 2 в нечетной степени (действительно один раз уже есть, и могут быть от у*у, но только в четных степенях, а один плюс четное - нечетно)
справа 2 если и есть то только в четной степени.
а 2 в нечетной степени не может быть равно 2 в четной
получили противоречие
Значит представления √2 в виде дроби не существует.
Таким образом число √2 - иррационально
P.S. использовано (два натуральных числа равны ⇔совпадают все степени простых сомножителей)
Пошаговое объяснение:
Задача на работу по формуле: A = P*t
Три неизвестных производительности - по именам - А, Д, И.
Пишем систему из трёх уравнений - производительность труда - скорость работы. Работа - А =1 - одна работа.
1) А + Д = 1/10 (1/ч) -
2) А + И = 1/8 (1/ч)
3) Д + И = 1/15 (1/ч)
А теперь СЛОЖИМ ВСЕ ТРИ УРАВНЕНИЯ и сразу немного упростим.
4) 2*(А + Д + И) = 1/10 + 1/8 + 1/15 (НОК 8,10,15= 120) = 7/24 (1/4 ч)
5) Рс = А+Д+И) = 7/24 : 2 = 7/48 (1/4) - совместная скорость работы
И находим время работы по формуле:
6) T = A/Pc = 1 : 7/48 = 48/7 = 6 6/7 часа работают вместе.
Переводим ответ в минуты.
6 6/7 ч = 48/7 ч *60 (мин/ч) = 2880/7 = 411 3/7 мин
Добавим им 25 сек на отдых - 4/7 минуты.
ответ: За 412 минут.
В решении.
Пошаговое объяснение:
1.
а) (3а + 4)² = 9а² + 24а + 16;
б) (2х - b)² = 4x² - 4xb + b²;
в) (b + 3)(b - 3) = b² - 9;
г) (5у - 2х)(5у + 2х) = 25у² - 4х².
2. (c + b)(c - b) - (5c² - b²) =
= c² - b² - 5c² + b² = -4c².
3.
a) 25у² - а² = (5у - а)(5у + а);
б) с² + 4bc + 4b² = (c + 2b)² = (c + 2b)(c + 2b).
4. 12 - (4 - х)² = х(3 - х)
12 - (16 - 8х + х²) = х(3 - х)
12 - 16 + 8х - х² = 3х - х²
8х - 3х - х² + х² = 4
5х = 4
х = 4/5
х = 0,8.
Проверка путём подстановки вычисленного значения х в уравнение показала, что данное решение удовлетворяет данному уравнению.
5.
а) (3х + у²)(3х - у²) = 9х² - у⁴;
б) (а³ - 6а)² = а⁶ - 12а⁴ + 36а²;
в) (а - х)²(х + а)² =
= (а² - 2ах + х²)(х² + 2ах + а²) =
=а²х² + 2а³х + а⁴ - 2ах³ - 4а²х² - 2а³х + х⁴ + 2ах³ + а²х² =
= а⁴ - 2а²х² + х⁴.
6.
а) 100а⁴ - 1/9 b² = (10a² - 1/3 b)(10a + 1/3 b);
б) 9х² - (х - 1)² = (3х - (х - 1))(3х + (х - 1) =
= (3х - х + 1)(3х + х - 1) =
= (2х + 1)(4х - 1);
в) х³ + у⁶ = (х + у²)(х² - ху² + у⁴).