Докажите, что число делится на 90.

Question

Математика: Докажите, что число делится на 90.

tayteldiyev2005 · Accepted Answer

Проведем радиус сферы в точку соприкосновения шара с цилиндром. Угол между этим радиусом и осью цилиндра (проходящего через центр сферы) обозначим как A.

Радиус оснвания цилиндра равен = R sin A

расстояние от центра сферы до основания цилиндра = R cos A

высота цилиндра в два раза больше расстояния от центра сферы до основания цилиндра, т.е. = 2R cos A

Значит объем цилиндра равен V = pi (R sin A)^2 * 2R cosA = pi R^3 * sin^2 A * cos A

Найдем максимум путем дифферинцирования ф-ции объема

V' = pi R^3 ([1-cos^2 A] cos A)'

$((1-\cos^2\alpha)\cos\alpha)' = (\cos\alpha-\cos^3\alpha)' =\\ = -\sin\alpha + 3\cos^2\alpha \sin\alpha =\\ =-\sin\alpha + (3-3\sin^2\alpha) \sin\alpha =\\ =-\sin\alpha + 3\sin\alpha - 3\sin^3\alpha = \sin\alpha (2 - 3\sin^2\alpha)$

т.е. максимум достигается при sin^2 A = 2/3

Объем сферы = 4/3 pi R^3

Отношение объемов = ( 4/3 pi R^3 ) / ( pi R^3 * sin^2 A * cos A ) = 4 / (3 * sin^2 A * cos A) =

2 / cos A = 2 sqrt(3)

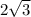
$2\sqrt{3}$

MOGZ ответил