Пошаговое объяснение: Раз они не делятся на 3 то каждое число в при делении на 3 будет давать остатки 1 или 2 теперь распишем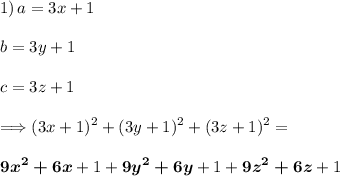 
можно заметить что выделенная часть всегда будет делится на 3 значит нам нужно только посмотреть на сумму единиц то есть 1+1+1=3 и поэтому число будет кратно трем Рассмотрим другой случай когда будут остатки 2 ; 1 ; 1 
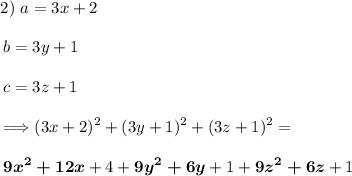тут также выделенная часть делится на 3 поэтому смотрим на сумму цифр 4+1+1=6 это число делится тоже на 3 дальше рассмотрим остатки 2;2;1 
тут аналогично выделенная часть делится на 3 смотрим на сумму цифр 4+4+1=9 это число делится на 3 в четвертом варианте где будут остатки 2;2;2 будет все аналогично первому нам нужно просто возвести 2-ку в квадрат и так двое там всего 3 то выйдет 2²*3=12 Вот мы и доказали что что число а²+в²+с² делится на 3
-3;-1;0;1;2
Пошаговое объяснение:
(n+3)/(n²+1) - целое число
Если ненулевая дробь равна целому числу, то ее знаменатель по модулю не превосходит числитель (случай равенства нулю рассматривается отдельно). Значит, |n+3|≥|n²+1| (*)
n²≥0 для любого n, а тогда n²+1>0 для любого n, откуда |n²+1|=n²+1
1) Пусть n+3<0 <=> n<-3
Тогда (*) равносильно -n-3≥n²+1 <=> n²+n+4≤0 <=> n²+2*n*(1/2)+(1/2)²+3+3/4≤0 <=> (n+(1/2))²+3+3/4≤0. Сумма неотрицательного и положительного выражений положительна - а значит неравенство решений не имеет.
2) Пусть n+3>0 <=> n>-3
Тогда (*) равносильно n+3≥n²+1 <=> n²-n-2≤0 <=> n²-2*n*(1/2)+(1/2)²-2-1/4≤0 <=> (n-(1/2))²≤(3/2)² <=> |n-(1/2)|≤3/2 <=> -1≤n≤2
Все полученные решения входят в рассматриваемую область.
3) Пусть n+3=0 <=> n=-3.
Знаменатель в ноль не обращается, а значит n=-3 - одно из искомых значений.
Остаётся найти на отрезке [-1;2] подходящие значения n.
Целых значений в данном случае всего 4, поэтому рациональнее обойтись перебором [в более сложных случаях придется продолжать анализ, например, используя делимость выражений: если знаменатель делится на какое-то число, а числитель нет, то, очевидно, целым числом дробь быть не может. И т.д.]
n=-1: 2/2=1 - подходит
n=0: 3/1=3 - подходит
n=1: 4/2=2 - подходит
n=2: 5/5=1 - подходит
Всего решили 28 примеров