начертите куб. проведите диагональ и плоскость. пусть длина ребра = a
пусть точка пересечения диагонали с плоскостью будет O.
для определения угла пересечения, необходимо из точки C1 опустить перпендикуляр к плоскости. Т.к. плоскость A1B1CD пересекает сторону CDB1C1 куба по диагонали CB1, то, следовательно, перпендикуляр будет проходить из точки C1 к прямой CB1. пусть точкой пересечения будет точка K на прямой CB1.
нужно найти tg угла C1OK, т.е. отношение C1K к KO.
Исходя из свойств симметрии куба, известно, что точка пересечения O будет находится в центре куба, деля длину ребра a пополам.
Т.е. KO = 0.5a
найдем C1K. из прямоугольного равнобедренного треугольника CKC1.
C1K = {корень квадратный} из (a в квадрате + a в квадрате) / 2 = a*{корень из 2}/2= a / {корень из 2}
tg угла C1OK = C1K / KO = a / {корень из 2} / 0.5 a = {корень из 2}
ответ: тангенс угла между диагональю куба AC1 и плоскости проходящей через вершины A1B1CD = {корень из 2}.
Простите великодушно за такое краткое решение, но тут залог верного решение - правильный чертеж и пространственное воображение, ну и знание формул, конечно.
а задачка - одна из наиболее сложных по данной теме
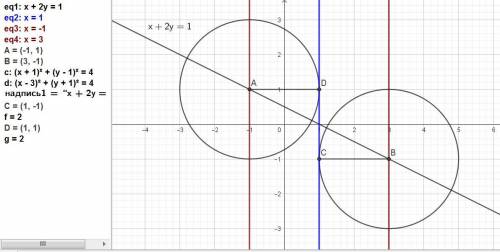
Так как не сказано, с какой стороны будет касание, то решений будет 2.
Так как заданная прямая, к которой будет касание, вертикальна, то центр окружности будет левее и правее её на величину радиуса, то есть появилось ещё одно условие расположения центра окружности.
Это будут прямые х = 1 - 2 = -1 и х = 1 + 2 = 3.
Находим координаты центров окружностей как точки пересечения заданной прямой x+2y-1=0 и двух найденных х = -1 и х = 3.
Подставляем значения х в уравнение прямой x+2y-1=0.
-1 + 2у -1 = 0,
2у = 2, у = 2/2 = 1.
Один центр найден: А(-1; 1).
Аналогично находим:
3 + 2у -1 = 0,
2у = -2, у = -2/2 = -1.
В(3; -1).
ответ: (x + 1)² + (y - 1)² = 2².
(x - 3)² + (y + 1)² = 2².
1) 984:4=246
2)246-2=244