
На прямую пропорциональность:
1) При равномерном движении поезд за 4 секунды метров. Сколько метров проедет поезд за 20 секунд?
Решение: 1) 20 : 4 = 5 (раз) во столько раз больше времени, значит и расстояние проедет в 5 раз больше.
2) 120 * 5 = 600 (м) - проедет поезд за 20 минут.
2) При равномерном движении поезд за 4 секунды метров. Сколько времени понадобиться ему, чтобы пройти расстояние 1км 200 м?
Решение: 1) 1200 : 120 = 10 (раз) - во столько раз больше нужно пройти, следовательно времени потребуется также в 10 раз больше.
2) 4 * 10 = 40 (с) - потребуется на прохождение 1км 200 м.
На обратно пропорциональную зависимость:
1) Поезд участок пути со скоростью 75 км/ч за 4 часа. За сколько часов поезд пройдет этот же участок пути, если будет двигаться со скоростью 100 км/ч?
Решение: 1) 75 * 4 = 300 (км) - путь, пройденный за 4 часа. Так как скорость увеличивается, то времени на прохождение того же участка пути понадобиться меньше.
2) 300 : 100 = 3 (часа) - время, необходимое на этот путь при скорости 100 км/ч.
2) Закупили 6 метров ткани по 50 рублей. Сколько ткани можно купить на эту же сумму по цене 75 рублей?
Решение: 1) 50 *6 = 300 (р) - стоимость покупки; С увеличением цены, количество купленной ткани уменьшается.
2) 300 : 75 = 4 (м) - ткани можно купить по цене 75 рублей.
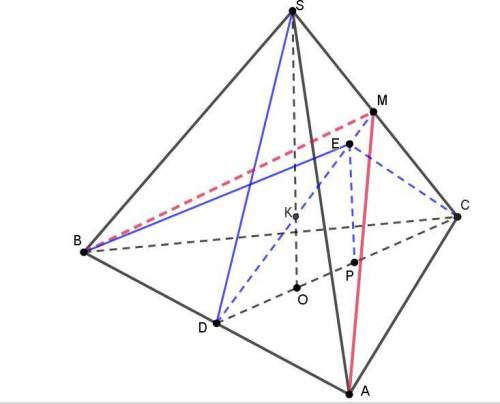
Эту задачу можно решить двумя
1) геометрическим,
2) векторным.
Пусть середина ребра AB - это точка D. Длину ребра основания примем равной 1.
1) Проведём вертикальную плоскость, проходящую через высоту пирамиды SO и высоту основания CD.
Отрезок МD в этой плоскости перпендикулярен АВ, поэтому угол МDС будет плоским углом между основанием пирамиды и плоскостью АМВ. Он равен 45 градусов.
Чтобы найти угол между прямой BC и плоскостью ABM, спроецируем отрезок ВС на плоскость АВМ.
Точка В останется на месте, а точка С попадёт в точку Е на прямой DМ.
В треугольнике DЕС сторона DС как высота основания равна √3/2.
Углы ЕDС и ЕСD равны по 45 градусов.
DЕ = СЕ = (1/2)DС*√2 = (1/2)*(√3/2)*√2 = √6/4.
Длину ВЕ найдём из прямоугольного треугольника ВЕD.
ВЕ = √((1/2)² + (√6/4)²) = √((1/4) + (6/16)) = √(5/8).
Находим косинус искомого угла ЕВС = α по теореме косинусов:
cos α = (1² + (√(5/8))² - (√6/4)²)/(2*1*√(5/8)) = √10/4.
ответ: α = arc cos(√10/4) = 0,6591 радиан = 37,761 градуса.
2) Поместим пирамиду в систему координат вершиной В в начало, ребром ВС по оси Оу.
По этому надо определить высоту точки М.
Пусть проекция точки М на СD это М1.
Так как точка М - середина SC, то DO = OM1 = (1/3)DC.
С учётом угла 45 градусов, DM1 = MM1 = (2/3)DC = (2/3)*(√3/2) = √3/3.
Получаем координаты точек.
А(√3/2; (1/2); 0), В(0; 0; 0), М(√3/12; 3/4; √3/3).
По трём точкам уравнение плоскости АВМ:
-0,2887x + 0,5y - 0,5774z + 0 = 0 .
Координаты точки С(0; 1; 0).
Вектор ВС:(0; 1; 0). Модуль 1 .
Вектор нормали плоскости имеет вид: А B C
Ax + By + Cz + D = 0 -0,2887 0,5 -0,5774
Модуль 0,8165 .
l m n Ск.произв. 0,5
0 1 0 Модуль 1 1
A B C sin fi = 0,612372436
-0,288675135 0,5 -0,577350269 Модуль 0,816496581
fi =0,659058036 радиан = 37,76124391 градус .