Рассмотрим слагаемое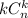 
, 
.
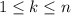Это количество сочетаний из 
элементов по 
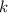, повторенное столько же раз.
Выстроим одну из комбинаций из 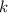элементов в строчку. Домножив на 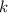, получим квадрат 
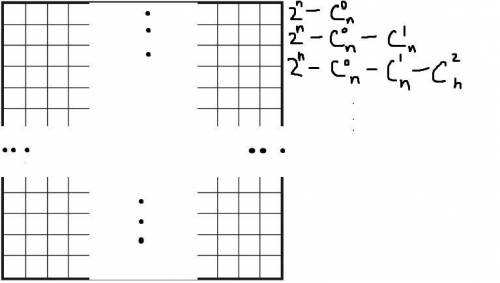
элементов. То есть 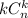— это множество квадратов. Теперь построим квадратную таблицу 
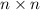(см.рис)
В первой строке будут первые строчки большинства квадратов, кроме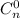 
. Во второй строчке уже не будет 
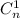, поскольку квадраты 
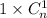целиком умещаются в первой строчке. И т.д. Причем будет отсутствовать вычитаемое 
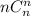, т.к. этот квадрат содержит все строчки.
Пусть искомая сумма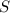 
. Сложив все строчки, получим 
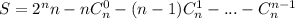, поскольку 
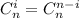, перепишем сумму:
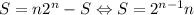
11/24, 1/2, 17/30, 20/19.
Пошаговое объяснение:
Рассмотрим внимательно дроби:
1. Наибольшей из дробей будет неправильная дробь 20/19 = 1 1/19. Она больше единицы, остальные являются правильными, каждая из них меньше единицы.
2. Оставшиеся правильные дроби можно сравнить двумя
1/2 = 60/120;
11/24 = 55/120;
17/30 = 68/120;
55/120 < 60/120 < 68/120, тогда и
11/24 < 1/2 < 17/30.
ответ: 11/24, 1/2, 17/30, 20/19.
11/24 < 12/24, 11/24 < 1/2,
17/30 > 15/30, 17/30 > 1/2,
получим, что
11/24 < 1/2 < 17/30.
ответ: 11/24, 1/2, 17/30, 20/19.