Решаем силой Разума - сначала думаем.
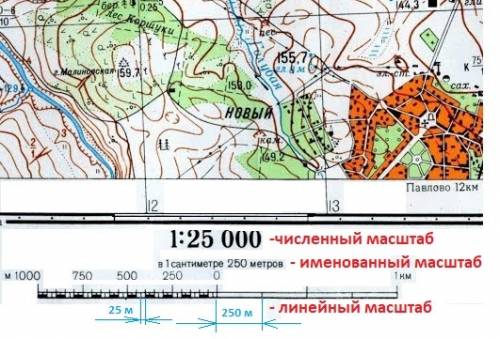
Мысль 1 - какие бывают масштабы? - на рисунке в приложении карта случайной местности. Три вида:численный, именованный, линейный.
Мысль 2 - как легче вычислять - делить или умножать.
Дано: М = 1:200 - численный масштаб,
N₁ = 7 м - реальный отрезок, N₂ = 5.2 м - реальный радиус.
Найти: L₁=? L₂=? Изобразить в масштабе.
Мысль 3 - вычислим через численный масштаб и умножаем.
1) L₁ = N₁ * M = 7(м)* (1/200) = 7/200 =0,035 (м) = 3,5 см = 35 мм. - длина отрезка - ответ.
Мысль 4 - вычислим через именованный масштаб, переведём в него и будем делить.
В 1 см = 200 см = 2 м или k = 2 м/см - именованный масштаб.
2) L₁ =N₁ : k = 7 (м) : 2 (м/см) = 3,5 см = 35 мм - длина отрезка - ответ - (гораздо проще оказалось).
Аналогично два варианта для задачи б) - радиус N₂ = 5,2 м.
3) L₂ = 5.2 (м) * 1/200 = 0,026 м = 2,6 см = 26 мм - радиус - ответ.
4) L₂ = 5.2 (м) : 2(м/см) = 2,6 см = 26 мм - радиус - ответ.
Мысль 5 - изображаем результаты на рисунке в приложении. Потребуется циркуль.
ДОПОЛНИТЕЛЬНО:
ИНТЕРЕСНА ОБРАТНАЯ ЗАДАЧА - как по карте или плану найти реальные размеры. Для этого можно использовать линейный нониус, который обычно есть на транспортире.
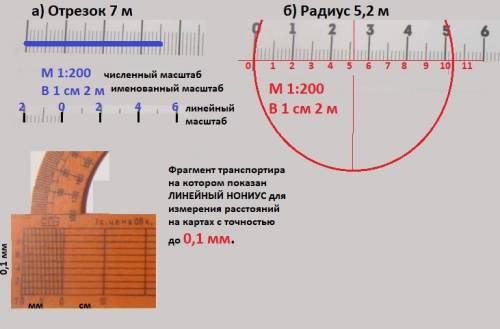
Расстояние между пунктами примем за единицу (целое).
1) 1 : 12 = 1/12 - часть пути, которую проедет почтовый поезд за 1 час;
2) 1 целая 1/3 = 3/3 + 1/3 = 4/3 (раз)
12 : 4/3 = 12 · 3/4 = 36/4 = 9 ч - время движения скорого поезда;
3) 1 : 9 = 1/9 - часть пути, которую проедет скорый поезд за 1 час;
4) 1/12 + 1/9 = 3/36 + 4/36 = 7/36 - часть пути, которую поезда проедут вместе за 1 час;
5) 1 : 7/36 = 1 · 36/7 = 36/7 = 5 целых 1/7 ч - время движения до встречи.
ответ: через 5 целых 1/7 ч поезда встретятся (≈ через 5 ч 9 мин).