1) припустимо, що площа першої ділянки становить х га.
2) тоді 0,4 х га становить площу другої ділянки і (х + 17) га — площа третьої ділянки.
3) (х + 0,4 х + (х + 17)) га-Загальна площа цих трьох земельних ділянок, що за умовою завдання становить 833 га. тому можливо записати:
х + 0,4 х + (х + 17) = 833.
4) вирішимо рівняння:
х + 0,4 х + х + 17 = 833;
2,4 х + 17 = 833;
2,4 х = 833 - 17;
2,4 х = 816;
х = 816 : 2,4;
х = 340.
5) знаходимо, що площа першої ділянки дорівнює 340 га.
6) обчислимо площі інших ділянок:
340 * 0,4 = 136 га — другого;
340 + 17 = 357 га — третього.
Відповідь: 340 га; 136 га і 357 га.
Пошаговое объяснение:
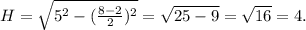
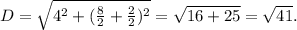
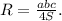
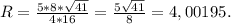
∠BAC = ∠CAD т.к. AC - биссектриса. ∠BCA = ∠CAD т.к. данный углы накрест лежащие при параллельных прямых. ⇒ ∠BAC = ∠CAD ⇒ ΔABC - равнобедренный. ⇒ AB = BC = СD (AB = CD т.к. трапеция равнобедренная) Пусть AB = BC = СD = x. Тогда 3х + 20 = 47 3х = 27 х = 9