Теорема Безу
Остаток от деления многочлена f(x) на двучлен (x - a) равен f(a)
Доказательство
f(x) = (x - a)·g(x) + r, где g(x) - частное, имеет степень на 1 меньше, чем f(x), а r - число (многочлен степени 0)
Тогда, подставляя x = a получаем:
f(a) = (a - a)·g(a) + r, то есть получаем f(a) = r, или r = f(a) - что и требовалось.
Теорема 2
x = a - корень f(x) ⇔ f(x) делится на (x - a)
Доказательство
из теоремы Безу получаем, что если f(a) = 0 (то есть a - корень f(x)) ⇒ f(x) = (x - a)·g(x) + 0 ⇒ f(x) при делении на (x - a) дает g(x) при 0-м остатке, а значит делится (x - a)
Обратно: раз f(x) делится на (x - a), значит остаток равен 0, а он по теореме Безу равен f(a), то есть a - корень f(x)
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
![\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/e1322.png)
Приведем к ступенчатому виду. Применяем операцию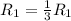 
к 
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию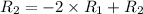 
к 
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию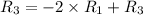 
к 
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/0d2b8.png)
Применяем операцию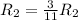 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/8a8f7.png)
Применяем операцию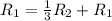 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/c212b.png)
Применяем операцию 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]](/tpl/images/1055/0577/960ac.png)
Применяем операцию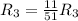 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/ffa18.png)
Применяем операцию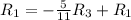 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/a5101.png)
Применяем операцию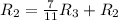 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]](/tpl/images/1055/0577/927aa.png)
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
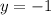
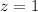
Решением является множество упорядоченных пар, которые удовлетворяют системе.
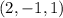
положительное, примеры
Правило деления с остатком целых отрицательных чисел, примеры
Проверка результата деления целых чисел с остатком
Статья разбирает понятие деления целых чисел с остатком. Докажем теорему о делимости целых чисел с остатком и просмотрим связи между делимыми и делителями, неполными частными и остатками. Рассмотрим правила, когда производится деление целых чисел с остатками, рассмотрев подробно на примерах. В конце решения выполним проверку.
Общее представление о делении целых чисел с остатками
Деление целых чисел с остатком рассматривается как обобщенное деление с остатком натуральных чисел. Это выполняется потому, что натуральные числа – это составная часть целых.
Деление с остатком произвольного числа говорит о том, что целое число a делится на число b, отличное от нуля. Если b=0, тогда не производят деление с остатком.
Также как и деление натуральных чисел с остатком, производится деление целых чисел a и b, при b отличном от нуля, на c и d. В этом случае a и b называют делимым и делителем, а d – остатком деления, с – целое число или неполное частное.