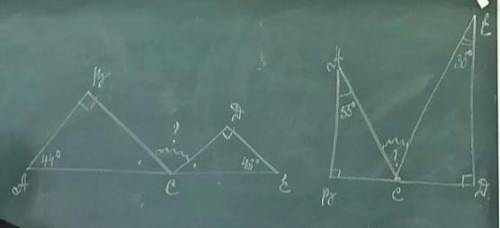
Для начала переведём все числа в неправильные дроби умножив знаменатель на целое число, а затем прибвавим числитель (для примера 1(целая) и 1/2 - это 2 умножить на 1 и +1. Получается 3/2).
13/5:(n+17/14)-7/5=1/3
Перенесём 1/3 в левую часть:
13/5:(n+17/14)-7/5-1/3=0
Приведём к общему знаменателю:
13/5:(n+17/14)-21/15-5/15=0
13/5:(n+17/14)-26/15=0
То же самое делаем с n:
13/5:((14n+17)/14)-26/15=0
Пользуемся свойством деления дробей (a/b:c/d=a/d*d/c):
13/5*(14/14n+17)-26/15=0
(182/(70n+85))-26/15=0
Накрест умножаем, перенеся в левую часть:
182*15=1820n+2210
n=2/7
Для начала переведём все числа в неправильные дроби умножив знаменатель на целое число, а затем прибвавим числитель (для примера 1(целая) и 1/2 - это 2 умножить на 1 и +1. Получается 3/2).
13/5:(n+17/14)-7/5=1/3
Перенесём 1/3 в левую часть:
13/5:(n+17/14)-7/5-1/3=0
Приведём к общему знаменателю:
13/5:(n+17/14)-21/15-5/15=0
13/5:(n+17/14)-26/15=0
То же самое делаем с n:
13/5:((14n+17)/14)-26/15=0
Пользуемся свойством деления дробей (a/b:c/d=a/d*d/c):
13/5*(14/14n+17)-26/15=0
(182/(70n+85))-26/15=0
Накрест умножаем, перенеся в левую часть:
182*15=1820n+2210
n=2/7
1)Т.к. сумма всех углов треугольника равна 180°, то <АСВ=180°-<ВАС-<АВС=180°-44°-90°=46°, а также <ДСЕ=180°-<СДЕ-<СЕД=180°-90°-49°=41°
<ВСД=180°-<АСВ-<ДСЕ=180°-46°-41°=93°(смежные)
ответ:<ВСД=93°.
2)Т.к. сумма всех углов треугольника равна 180°, то <АСВ=180°-<ВАС-<АВС=180°-55°-90°=35°, а также <ДСЕ=180°-<СДЕ-<СЕД=180°-90°-35°=55°
<АСЕ=180°-<АСВ-<ДСЕ=180°-35°-55°=90°(смежные)
ответ:<АСЕ=90°.