Комбинаторные задачи Решить задачи

В школьной столовой на первое можно заказать борщ, солянку, грибной суп, на второе - мясо с макаронами, рыбу с картошкой, курицу с рисом, а на третье - чай и компот. Сколько различных обедов можно составить из указанных блюд?
В ювелирную мастерскую привезли 6 изумрудов, 9 алмазов и 7 сапфиров. Ювелиру заказали браслет, в котором 3 изумруда, 5 алмазов и 2 сапфиров. Сколькими он может выбрать камни на браслет?
В районе построили новую школу. Из пришедших 25 человек нужно выбрать директора школы, завуча начальной школы, завуча среднего звена и завуча по воспитательной работе. Сколькими это можно сделать?
В кабинете заведующего ювелирного магазина имеется код, состоящий из двух различных гласных букв русского алфавита, за которой следуют 3 различные цифры. Сколько вариантов придется перебрать мошеннику, чтобы раздобыть драгоценности, которые там хранятся?
Сколькими из колоды в 36 карт можно выбрать 3 карты?
В студенческой группе 23 человека. Сколькими можно выбрать старосту и его заместителя?
В лифт 12-этажного дома сели 3 пассажира. Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со 2-го) этаже. Сколькими :
пассажиры могут выйти на одном этаже;
два человека могут выйти на одном этаже, а третий – на другом;
люди могут выйти на разных этажах;
пассажиры могут выйти из лифта?
8. Сколько различных слов (не обязательно осмысленных) можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?

9. Алексей занимается спортом, причём 4 дня в неделю – лёгкой атлетикой, 2 дня – силовыми упражнениями и 1 день отдыхает. Сколькими он может составить себе расписание занятий на неделю?

10.Сколько существует четырёхзначных пин-кодов?

11. При встрече каждый из друзей другому руку. Сколько всего было рукопожатий, если встретились 6 друзей?

12. Сколько существует вариантов рассаживания вокруг стола 6 гостей на 6 стульях?

13. Пятеро друзей сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно?

14. Сколькими 10 футбольных команд могут разыграть между собой золотые, бронзовые и серебряные медали?

15. Имеется 6 видов овощей. Решено готовить салаты из трёх видов овощей. Сколько различных вариантов салатов можно приготови

👇

Открыть все ответы

Ответ:

korzhik559

13.03.2023

Привести квадратичную форму к каноническому виду методом Лагранжа
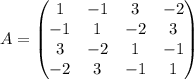
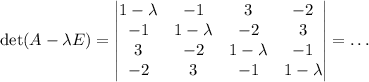
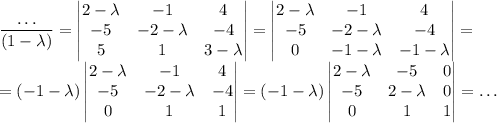
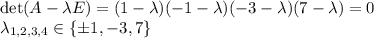
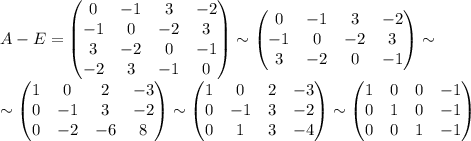
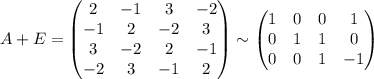
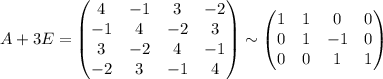
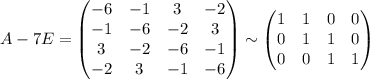
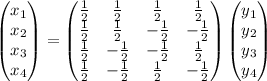
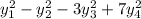
x² + 10xy + 2xz - z²

Решение
Метод Лагранжа - это просто метод выделения полных квадратов.
Собираем все слагаемые с переменной x

x² + 10xy + 2xz - z² = (x² + 10xy + 2xz) - z² =
= (x² + 2x*5y + 25y² - 25y² + 2xz + z² - z²) - z² =
= (x² + 2x*5y + 25y² + 2xz + z² ) - 25y² - z² - z² =
= (x + 5y + z)² - 25y² - 2z²
обозначаем : x' = x + 5y + z; y' = y; z' =z
(где x = x' - 5y' - z'; y = y'; z = z')

x² + 10xy + 2xz - z² = (x + 5y + z)² - 25y² - 2z² = x'² - 25y'² - 2z'²
Получили канонический вид.

4,6(49 оценок)

Ответ:

RstneaLeu

13.03.2023

Матрица, соответствующая данной квадратичной форме:
$A=\begin{pmatrix}
 1 & -1 & 3 & -2 \\
 -1 & 1 & -2 & 3 \\
 3 & -2 & 1 & -1 \\
 -2 & 3 & -1 & 1 
\end{pmatrix}$

Нужно найти собственные числа и собственные вектора этой матрицы. Собственные числа находим из уравнения det(A - λE) = 0:
$\det (A-\lambda E)=\begin{vmatrix}1-\lambda & -1 & 3 & -2 \\ -1 & 1-\lambda & -2 & 3 \\ 3 & -2 & 1-\lambda & -1 \\ -2 & 3 & -1 & 1-\lambda\end{vmatrix}=\dots$

Прибавим к первой строке все остальные строки, после вынесения общего множителя обнулим первый столбик во всех строках, кроме первой:
$\dots=\begin{vmatrix}1-\lambda & 1-\lambda & 1-\lambda & 1-\lambda \\ -1 & 1-\lambda & -2 & 3 \\ 3 & -2 & 1-\lambda & -1 \\ -2 & 3 & -1 & 1-\lambda\end{vmatrix}=\\=(1-\lambda)\begin{vmatrix}1 & 1 & 1 & 1 \\ -1 & 1-\lambda & -2 & 3 \\ 3 & -2 & 1-\lambda & -1 \\ -2 & 3 & -1 & 1-\lambda\end{vmatrix}=\\=(1-\lambda)\begin{vmatrix}1 & 1 & 1 & 1 \\ 0 & 2-\lambda & -1 & 4 \\ 0 & -5 & -2-\lambda & -4 \\ 0 & 5 & 1 & 3-\lambda\end{vmatrix}=\dots$

Раскладываем определитель по первому столбцу. Опустим пока множитель (1 - λ), сложим прибавим к третьей строчке вторую, вынесем общий множитель и обнулим третий столбец везде, кроме последней строки:
$\dfrac{\dots}{(1-\lambda)}=\begin{vmatrix}2-\lambda & -1 & 4 \\ -5 & -2-\lambda & -4 \\ 5 & 1 & 3-\lambda\end{vmatrix}=\begin{vmatrix}2-\lambda & -1 & 4 \\ -5 & -2-\lambda & -4 \\ 0 & -1-\lambda & -1-\lambda\end{vmatrix}=\\=(-1-\lambda)\begin{vmatrix}2-\lambda & -1 & 4 \\ -5 & -2-\lambda & -4 \\ 0 & 1 & 1\end{vmatrix}=(-1-\lambda)\begin{vmatrix}2-\lambda & -5 & 0 \\ -5 & 2-\lambda & 0 \\ 0 & 1 & 1\end{vmatrix}=\dots$

Раскладываем определитель по третьему столбцу, после отбрасывания множителей остается определитель матрицы 2x2, который равен
$(2-\lambda)^2-(-5)^2=(-3-\lambda)(7-\lambda)$

Итак,
$\det (A-\lambda E)=(1-\lambda)(-1-\lambda)(-3-\lambda)(7-\lambda)=0\\
\lambda_{1,2,3,4}\in\{\pm 1,-3,7\}$

Находим собственные векторы:
1) с.ч. = 1
Сумма всех строк равна 0, выкинем последнюю. Приведем матрицу к красивому виду (насколько сможем):
$A-E=\begin{pmatrix} 0 & -1 & 3 & -2 \\ -1 & 0 & -2 & 3 \\ 3 & -2 & 0 & -1 \\ -2 & 3 & -1 & 0 \end{pmatrix}\sim \begin{pmatrix} 0 & -1 & 3 & -2 \\ -1 & 0 & -2 & 3 \\ 3 & -2 & 0 & -1 \end{pmatrix}\sim \\\sim \begin{pmatrix} 1 & 0 & 2 & -3 \\ 0 & -1 & 3 & -2 \\ 0 & -2 & -6 & 8 \end{pmatrix} \sim \begin{pmatrix} 1 & 0 & 2 & -3 \\ 0 & -1 & 3 & -2 \\ 0 & 1 & 3 & -4 \end{pmatrix} \sim \begin{pmatrix} 1 & 0 & 0 & -1 \\ 0 & 1 & 0 & -1 \\ 0 & 0 & 1 & -1 \end{pmatrix}$

Из полученного вида матрицы получаем, что уравнению удовлетворяют все вектора вида (a, a, a, a); с.в. (1, 1, 1, 1)

2) c.ч. = -1
$A+E=\begin{pmatrix} 2 & -1 & 3 & -2 \\ -1 & 2 & -2 & 3 \\ 3 & -2 & 2 & -1 \\ -2 & 3 & -1 & 2 \end{pmatrix}\sim \begin{pmatrix} 1&0&0&1\\0 & 1 & 1 & 0 \\ 0 & 0 & 1 & -1 \end{pmatrix}$
с.в. (1, 1, -1, -1)

3) с.ч. = -3
$A+3E=\begin{pmatrix} 4 & -1 & 3 & -2 \\ -1 & 4 & -2 & 3 \\ 3 & -2 & 4 & -1 \\ -2 & 3 & -1 & 4 \end{pmatrix}\sim \begin{pmatrix} 1&1&0&0\\0 & 1 & -1 & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix}$
с.в. (1, -1, -1, 1)

4) с.ч. = 7
$A-7E=\begin{pmatrix} -6 & -1 & 3 & -2 \\ -1 & -6 & -2 & 3 \\ 3 & -2 & -6 & -1 \\ -2 & 3 & -1 & -6 \end{pmatrix}\sim \begin{pmatrix} 1&1&0&0\\0 & 1 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{pmatrix}$
c.в. (1, -1, 1, -1)

Собственные вектора уже ортогональны, но еще не отнормированы. Длина каждого равна 1/2, так что окончательно получаем, что под действием замены
$\begin{pmatrix}x_1\\x_2\\x_3\\x_4\end{pmatrix}=\begin{pmatrix}\frac12&\frac12&\frac12&\frac12\\\frac12&\frac12&-\frac12&-\frac12\\\frac12&-\frac12&-\frac12&\frac12\\\frac12&-\frac12&\frac12&-\frac12\end{pmatrix}\begin{pmatrix}y_1\\y_2\\y_3\\y_4\end{pmatrix}$
(по столбцам записаны собственные векторы) квадратичная форма примет вид
y_1^2-y_2^2-3y_3^2+7y_4^2