Диагональное сечение пирамиды представляет собой треугольник, основание которого есть диагональ квадрата, лежащего в основании пирамиды, а высота - есть высота пирамиды.Найдём диагональ квадрата со стороной а = 14 см
D = √(2а²) = а√2 = 14√2 (см)
Чтобы найти высоту пирамиды, надо рассмотреть прямоугольный тр-к. образованный боковым ребром р = 10, высотой Н и половинкой диагонали 0,5D = 7√2 квадратного основания. Н = √(р² -(0,5D)²) = √(100- 49·2) = √2 (см)
Ну, и наконец, площадь дагонального сечения
S = 0,5·D·Н = 0,5·14√2·√2 = 14(см²)
Правильная четырехугольная пирамида 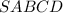 .
.
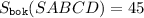 (см²).
(см²).
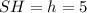 (см).
(см).
 - сторону основания.
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
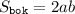 , где
, где  - сторона основания и
- сторона основания и 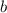 - апофема (высота боковой грани, проведенная из вершины).
- апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить 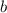 через
через  (сторону основания) и
(сторону основания) и 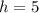 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный 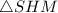 (где
(где 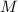 - середина
- середина 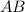 ). В нем
). В нем 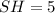 (см), а
(см), а 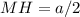 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
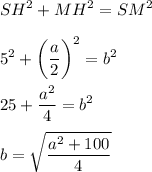
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что  - неотрицательное):
- неотрицательное):
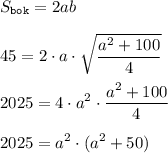
Пусть 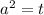 :
:
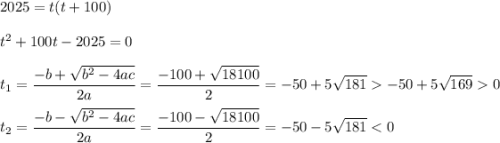
Второй корень нам не подходит по причине отрицательности. Значит:
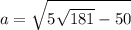
Задача решена!
ответ: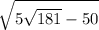 или около
или около 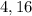 (см).
(см). 
1час=60мин
18/60=3/20 час
Первый велосипедист – Х+3
Второй велосипедист – Х
t – час
Х+(Х×3/20)+(Х+3)=46
2 3/20Х+3=46
2,15Х=46-3
2,15Х=43
Х=20
Тогда –
Первый велосипедист – 23 км/час
Второй велосипедист – 20 км/час
Проверка:
20+(20×3/20)+(20+3)=46
20+3+20+3=46
40+6=46
46=46