
Числа A и B называются взаимно простыми, если НОД(А; В)=1.
Возможны различные варианты :
а) Если числа А и В простые, то НОД(А; В)=1. Например:
НОД(2; 3)=1, НОД(2; 5)=1, НОД(3; 7)=1.
1) 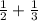
Так как НОД(2; 3)=1, то НОК(2; 3)=2·3=6
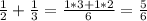
2) 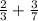
НОД(3; 7)=1, то НОК(3; 7)=3·7=21
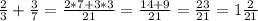
б) Если числа А и В составные, но не имеют одинаковых простых делителей, тогда НОД(А; В)=1. Например:
НОД(4; 9)=1, НОД(4; 25)=1, НОД(9; 16)=1.
3) 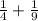
Так как НОД(4; 9)=1, то НОК(4; 9)=4·9=36
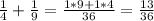
2) 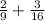
НОД(9; 16)=1, то НОК(9; 16)=9·16=144
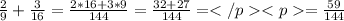
В общем случае, если А и В взаимно простые, то есть
НОД(А; В)=1, то НОК(А; В)=А·В.
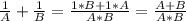
Пошаговое объяснение:
1) а1 = 14 d= -7
a15 = a1 + 14d = 14 + 14 *(-7) = 14 - 98 = - 84
2) a1 = -9 a2= -6 a3 = - 3
d = a2 - a1= -6 -(-9) = - 6 + 9 = 3
S6= (a1+d(n-1)/2))*n = (-9 + 3* 5)/2)) * 6 = 3 * 6 = 18
3)an = 5n - 8
a1 = 5* 1 - 8 = -3
a30 = 5n -8 = 5 * 30 - 8 = 150 - 8 = 142
Подставляем в формулу суммы и вычисляем:
S30 = 30 * (a1 + a30)/2 = 15 * (a1 + a30) = 15 * (-3 + 142) = 15 * 139 = 2085
4) Из формулы n–го члена, найдем разность арифметической прогрессии.
a6 = a1 + d(6-1)
17 = 7 + 5d
10 = 5d
d = 2
56 = 7 + 2(n- 1)
56 = 7 + 2n -2
-2n = 5 - 56
- 2n = -51
n= - 51 : (-2)
n= 25,5 десятичная дробь, поэтому 56 не может быть членом данной арифметической прогрессии.