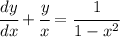
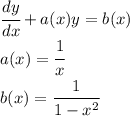
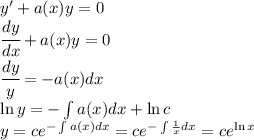
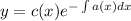
![y=ce^{-\int a(x)dx}=ce^{-\int\frac{1}{x}dx}=ce^{\ln x}\\y=c(x)e^{-\int a(x)dx}\\c'(x)e^{-\int a(x)dx}+c(x)e^{-\int a(x)dx}\cdot (-a(x))+a(x)c(x)e^{-\int a(x)dx}=b(x)\\c'(x)=b(x)e^{\int a(x)dx}\\c(x)=\int b(x)e^{\int a(x)dx}+C_1\\y=c(x)e^{-\int a(x)dx}=\left[\int b(x)e^{\int a(x)dx}dx+C_1\right]e^{-\int a(x)dx](/tpl/images/0177/2092/9f4c9.png)
![y=c(x)e^{-\int a(x)dx}=\left[\int b(x)e^{\int a(x)dx}dx+C_1\right]e^{-\int a(x)dx\\y}=\\=\left[\int\cfrac{1}{1-x^2}e^{\ln x}+C_1\right]e^{\ln x}=\left[\int\cfrac{x}{1-x^2}+C_1\right]x=\\=\left[-\cfrac{1}{2}\ln (1-x^2)+C_1\right]x](/tpl/images/0177/2092/c8406.png)
Обозначим скорости велосипедистов x км/ч и y км/ч.
Они за 1 час проехали вместе 25 км и встретились, значит, сумма их скоростей равна 25 км/ч.
x + y = 25; y = 25 - x
Один проезжает 30 км на 1 час быстрее другого.
Если один со скоростью x км/ч проезжает 30 км за t = 30/x часов.
Второй, со скоростью y км/ч проезжает на 1 час медленнее, то есть за
30/y = t - 1 = 30/x - 1
30/y = (30 - x)/x
Подставляем 1 уравнение во 2 уравнение
30/(25 - x) = (30 - x)/x
По правилу пропорции
30x = (30 - x)(25 - x) = x^2 - 55x + 750
x^2 - 85x + 750 = 0
(x - 75)(x - 10) = 0
x = 75 > 25 - не подходит
x = 10 км/ч; y = 25 - x = 25 - 10 = 15 км/ч.
Перепишем в таком виде:
( dy(x))/( dx)+(y(x))/x = -1/(x^2-1)
Положим mu(x) = e^( integral 1/x dx) = x.
Умножим обе части на mu(x):
x ( dy(x))/( dx)+y(x) = -x/(x^2-1)
заменим 1 = ( d)/( dx)(x):
x ( dy(x))/( dx)+( d)/( dx)(x) y(x) = -x/(x^2-1)
Применим g ( df)/( dx)+f ( dg)/( dx) = ( d)/( dx)(f g) к левой части:
( d)/( dx)(x y(x)) = -x/(x^2-1)
Проинтегрируем обе части по x:
integral ( d)/( dx)(x y(x)) dx = integral -x/(x^2-1) dx
Получаем:
x y(x) = -1/2 log(x^2-1)+c_1, где c_1 произвольная константа.
Разделим обе части на mu(x) = x:
ответ: | | y(x) = (-1/2 log(x^2-1)+c_1)/x